Zvuková technika a elektroakustika (zvuková technika + elektrotechnika)

Kapitola10

Prostorová akustika

Jedná se o obor zabývající se optimální akustikou uzavřeného prostoru tak, aby prostor plnil z akustického hlediska svůj účel. Existuje několik metod analýzy prostorové akustiky (např. vlnová nebo geometrická akustika). V této kapitole se omezíme na tzv. statistickou akustiku.

Poznámka

Statistická akustika se omezuje na uzavřené prostory. Předpokládá, že je intenzita zvuku ve všech místech uzavřeného prostoru stejná (objemová hustota zvukové energie je konstantní), všechny úhly dopadu zvukových vln do libovolných bodů jsou stejně pravděpodobné a že v každém místě prostoru je celková energie dána součtem středních hodnot všech energií, které do zvoleného bodu dospěly díky odrazům od stěn.

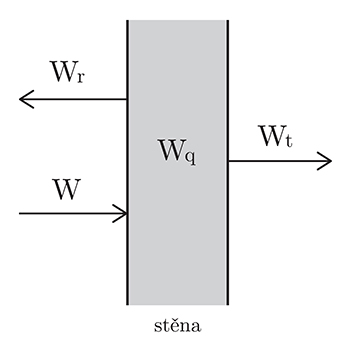
Dopadem zvukové vlny na stěnu dochází z části k pohlcení energie stěnou, z části k jejímu odrazu (viz obr. 89). Celkovou energii zvukové vlny dopadající na stěnu tak lze popsat vztahem (28):

W = W_{r} + W_{a}

kde

W

je celková energie,

W_{r}

je energie odražená a

W_{a}

je energie pohlcená stěnou. Vzhledem k tomu, že část pohlcené energie se vyzáří do prostoru za zdí, platí následující vztah (29):

W_{a} = W_{q} + W_{t}

kde

W_{q}

je energie přeměněná na teplo a

W_{t}

je energie vyzářená do prostoru za stěnou.

Obr. 89. Schéma odrazu zvukové vlny při dopadu na stěnu

Pohlcování zvukové energie lze popsat činitelem zvukové pohltivosti

α

. Jedná se o bezrozměrné číslo udávající poměr pohlcené energie vůči energii dopadlé (30):

α = \frac{W_{a}}{W_{i}}

[–]

Konkrétní hodnota činitele zvukové pohltivosti konkrétního materiálu se stanovuje ze vzorku materiálu dle platných norem akustickým měřením v impedanční trubici (interferometru). Nabývá hodnot mezi 0 a 1.

Rozlišujeme tyto typy materiálů:

Porézní materiály – energie procházející zvukové vlny se třením ve struktuře porézního materiálů mění na teplo. Pohlcení delších vlnových délek lze dosáhnout úměrným zvýšením tloušťky materiálu. Příkladem materiálu je akustická pěna (viz obr. 90), minerální vata nebo filc.

Obr. 90. Porézní materiál ve formě akustického obkladu

Rezonanční absorbéry – jsou tvořeny mechanickým oscilátorem, např. tuhou děrovanou deskou umístěnou před stěnou v určité vzdálenosti odpovídající pohlcované vlnové délce. Po prostupu zvukové vlny dutinou desky začne v prostoru mezi deskou a stěnou rezonovat a tím zanikat (v důsledku postupné přeměny na teplo). Rozšíření pohlcovaného kmitočtového rozsahu lze docílit vyplněním vzduchové mezery porézním materiálem.

Samostatné absorbéry – jedná se o volné objekty v prostoru. V případě kinosálu jde o židle, sedačky, diváky apod.

Zajímavost

Při navrhování sedaček do kinosálu platí, že pohltivost neobsazené sedačky by měla být přibližně stejná jako pohltivost obsazené sedačky. Zabraňuje se tím změnám akustických vlastností při různém zaplnění kinosálu.

V případě difúzního odrazu (definovaného v kapitole 8.1) se část energie rozptýlí do prostoru. Tohoto principu s výhodou využívají difuzory. Ty se umísťují na stěny z důvodu prevence vzniku stojatých vln, které by významně ovlivnily akustické vlastnosti poslechového prostoru. Po dopadu zvukové vlny na difuzor dochází vzhledem k neuspořádanosti jeho struktury k rozbití zvukové vlny do prostoru, tedy jejímu odrazu do všech směrů. Příklad difuzoru použitého v hudebním studiu je na obr. 92.

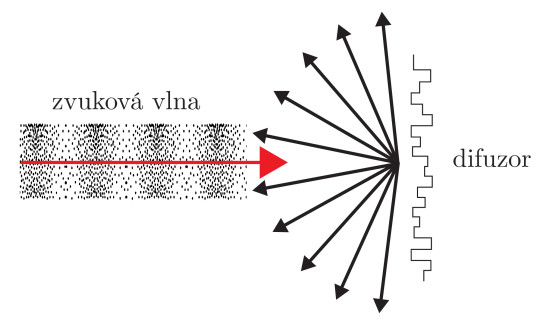
Obr. 91. Princip rozptylu zvukové vlny pomocí difuzoru

Obr. 92. Studiový difuzor

Uzavřený prostor je specifický odrazy zvukových vln od stěn. V tomto prostoru tak bude hladina akustické intenzity vyšší než ve volném poli. V uzavřeném prostoru se totiž část zvukové energie udržuje, kdežto ve volném poli se šíří do nekonečna. Volné pole lze proto považovat za uzavřený prostor s dokonale pohltivými stěnami.

Blízkým polem rozumíme těsnou vzdálenost od zdroje zvuku, kdy akustická intenzita není přímo vztažena k hodnotě akustického tlaku. Akustické veličiny jsou zde obtížně měřitelné a pro poslech není toto pole vhodné. V případě kina toto pole neuvažujeme.

Za blízkým polem se vytváří tzv. vzdálené pole. V uzavřeném prostoru v něm v určitých místech převládají přímé vlny a v jiných se uplatňují větší měrou odražené vlny (dozvukové pole).

Od určité vzdálenosti od zdroje dochází k rovnoměrnému rozložení zvukové energie v prostoru a tím vzniku tzv. difúzního pole. V takovém poli již není možné určit směr šíření dílčích vln, neboť přicházejí ze všech směrů se stejnou pravděpodobností. Prostor je tedy nasycen zvukovou energií.

Hranici mezi volným a difúzním polem udává tzv. poloměr doznívání (31):

r_{d} = 0,057 \sqrt{\frac{V}{T}}

[s]

kde V je objem prostoru a T je doba dozvuku. Ze vzorce je patrné, že poloměr doznívání je díky době dozvuku závislý na kmitočtu.

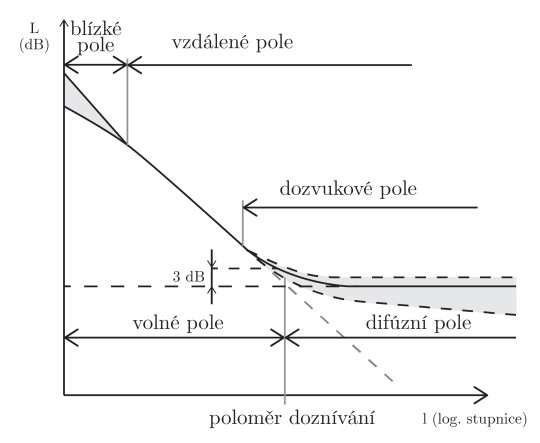
Obr. 93.Typy akustických polí v uzavřeném prostoru v závislosti na vzdálenosti od zdroje

V difúzním poli se uplatňuje doba dozvuku. Po určité době od vypnutí zdroje zvuku dochází vlivem mnohonásobných odrazů zvukových vln od stěn prostoru k jejich postupnému zanikání. Doba dozvuku je definována jako doba, za kterou poklesne hustota zvukové energie po vypnutí zdroje na

10^{- 6}

původní hodnoty, tedy o 60 dB.

Příklad

Požadavky na dobu dozvuku pro kinosály se řídí normami a je závislá na objemu sálu a pohltivosti jeho stěn. Obecně by se doba dozvuku měla pohybovat v řádu desetin sekundy, tedy cca 750 ms. Tato doba dozvuku je oproti normám pro jiné druhy místnosti poměrně krátká. Dozvuk by měl být dán uměleckým záměrem autora filmu, nikoliv akustickými vlastnostmi poslechového prostoru.

Způsoby měření doby dozvuku jsou uvedeny v kapitole 14. Pro výpočet této doby se využívá nejčastěji Sabinova vzorce (32):

T_{D} = 0,164 \frac{V}{α S}

[s]

kde V je objem prostoru, α je činitel pohltivosti a S je celková plocha stěn. Činitel pohltivosti v tomto případě vyjadřuje celkovou pohltivost všech ohraničujících ploch

S_{i}

, které vykazují dílčí hodnoty činitele pohltivosti

α_{i}

. Průměrná hodnota se vypočítá vztahem (33):

α = \frac{\sum_{i} α_{i} S_{i}}{S}

[–]

kde celkový povrch stěn S dán součtem všech

S_{i}

Poznámka

Sabinův vztah pro výpočet doby dozvuku má omezené podmínky používání. Pokud je pohltivost stěn nulová (

α = 0

), vychází doba dozvuku nekonečná. Vzorec totiž neuvažuje útlum zvuku při jeho šíření prostorem. V případě dokonalé pohltivosti stěn (

α =

1) vychází doba dozvuku jako nenulová, i když by nulová být měla. Pro vyšší hodnoty pohltivosti (např. v zatlumených kinosálech) se proto uplatňuje Eyringův vztah pro výpočet doby dozvuku. Pro běžné výpočty, aplikace a rutinní měření doby dozvuku v akustice však zpravidla vždy postačuje Sabinův vztah.

Eyringův vztah pro výpočet doby dozvuku je následující (34):

T_{D} = 0,164 \frac{V}{- S \ln (1 - α)} [s]

kde činitel pohltivosti α se vypočte vzorcem (35):

α = \frac{α_{1} S_{1} + α_{2} S_{2} + \dots + α_{n} S_{n}}{S}

kde

α_{i}

jsou činitelé pohltivosti jednotlivých stěn a

S_{i}

jsou jejich plochy.

Po zapnutí zdroje zvuku hustota zvukové energie v prostoru postupně narůstá. Postupně se zvyšuje také výkon pohlcovaný stěnami. Ustálení je charakterizováno momentem vyrovnání množství generované energie zdrojem s množstvím pohlcené energie. Tento časový interval se označuje pojmem doba názvuku. Jedná se o časový interval, za který dosáhne hustota zvukové energie hodnoty

1 - \frac{1}{e}

, tedy 63 % ustálené hodnoty. Odpovídá vztahu (36):

T_{n} = \frac{4 \cdot V}{α \cdot c \cdot S} [s]

kde V je objem prostoru, α je činitel pohltivosti, c je rychlost šíření zvuku a S je celková plocha stěn.