Projekce klasické filmové kopie (filmová optika + filmová kopie)

1.3

Zákony geometrické optiky

Přímočarost šíření – Optický paprsek urazí mezi dvěma body nejkratší možnou vzdálenost.

Odraz paprsků – Dopadá-li paprsek na rozhraní dvou prostředí a nevstoupí-li do druhého prostředí kompletně nebo jen z části, dochází k odrazu paprsku ve stejné rovině jako dopadající paprsek a platí, že úhel dopadu je roven úhlu odrazu.

Lom paprsků – Dopadá-li paprsek na rozhraní dvou prostředí charakterizovaných indexy lomu $n_{1}$ a $n_{2}$ a vstoupí-li tento paprsek do druhého prostředí kompletně nebo jen z části, dochází k lomu paprsku ve stejné rovině jako dopadající paprsek, přičemž platí rovnice (5):
$n_{1} \cdot s i n α_{D} = n_{2} \cdot s i n α_{L}$ ,
kde $n_{1}$ a $n_{2}$ jsou indexy lomu obou prostředí a $α_{D}$ a $α_{L}$ jsou úhly dopadu a lomu paprsku (viz obr.

Obr. 3. Lom světelných paprsků na rozhraní dvou různých prostředí

V případě dvou elektricky nevodivých prostředí charakterizovaných relativními permitivitami

ε_{r 1}

ε_{r 2}

a relativními permeabilitami

μ_{r 1}

μ_{r 1}

s dokonale rovným rozhraním lze z rovnic (1) a (2) odvodit relativní index lomu jako vzájemný podíl rychlostí šíření světelných paprsků v obou prostředích (6):

n_{12} = \frac{v_{1}}{v_{2}} = \frac{\sqrt{ε_{0} ε_{r 2} μ_{0} μ_{r 2}}}{\sqrt{ε_{0} ε_{r 1} μ_{0} μ_{r 1}}} = \frac{c \cdot \sqrt{ε_{r 2} μ_{r 2}}}{c \cdot \sqrt{ε_{r 1} μ_{r 1}}} = \frac{\sqrt{ε_{r 2} μ_{r 2}}}{\sqrt{ε_{r 1} μ_{r 1}}}

Pokud je jedno z prostředí vakuum, hovoří se o absolutním indexu lomu (7):

n = \frac{c}{v} = \sqrt{ε_{r} μ_{r}}

Hmotnější prostředí, tedy prostředí s vyšším indexem lomu, je považováno za opticky hustší. Méně hmotné prostředí, mající nižší index lomu než hmotnější prostředí, je považováno za opticky řidší. V takovém prostředí se fotony šíří rychleji než v opticky hustším prostředí.

Snellův zákon lomu, platící na rozhraní dvou prostředí, popisuje způsob lomu paprsku. Proniká-li paprsek z prostředí opticky řidšího do prostředí opticky hustšího, paprsky se lámou ke kolmici. Proniká-li paprsek z prostředí opticky hustšího do prostředí opticky řidšího, paprsek se láme od kolmice. V tomto případě může při překročení mezního úhlu

α_{m}

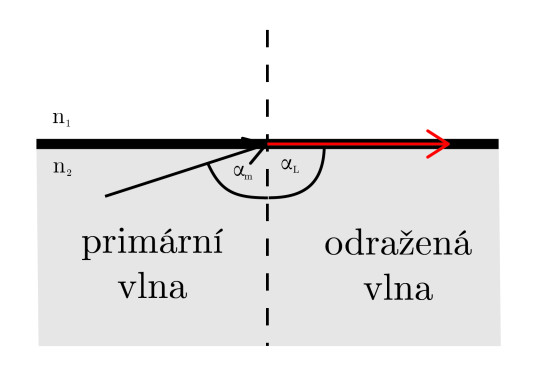
(viz obr. 4) dojít k tzv. totálnímu odrazu, kdy se světlo odrazí zpět do prostředí opticky hustšího (viz obr. 5). Výpočet konkrétní hodnoty mezního úhlu je odvozen z rovnice (5).

Obr. 4. Lom paprsku pod mezním úhlem α_m

Příklad

Odvoďte hodnotu mezního úhlu dopadu pro úhel lomu

α_{L} = 90 °

s využitím Snellova zákona (rovnice (5)).

Zobrazit řešení

Skrýt řešení

Řešení

n_{1} \cdot s i n α_{D} = n_{2} \cdot s i n α_{L}

n_{1} \cdot s i n α_{D} = n_{2} \cdot s i n \frac{π}{2}

n_{1} \cdot s i n α_{D} = n_{2} \cdot 1

s i n α_{D} = \frac{n_{2}}{n_{1}}

α_{m} = a r c s i n \frac{n_{2}}{n_{1}}

V případě nerovného rozhraní dvou prostředí může nastat difúzní odraz neboli rozptýlení jednotlivých paprsků do různých směrů. Tento jev nastává například na vodní hladině.

Poznámka

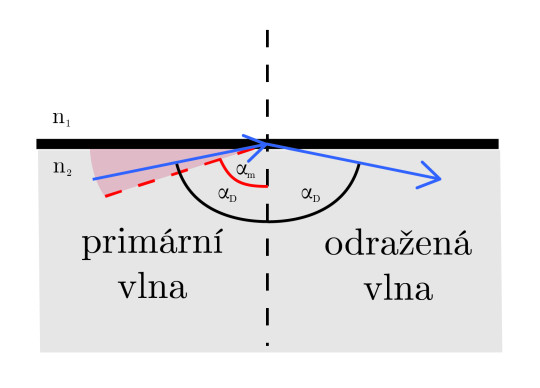
Totálního odrazu (na obr. 5) se využívá v optických vláknech. To tvoří jádro z opticky hustšího materiálu (typicky sklo nebo tvrzený plast) a obal z opticky řidšího materiálu (plast). Při instalaci optických vláken je nutností dodržet maximální povolený ohyb vlákna, který je závislý na hodnotě mezního úhlu. V případě jeho překročení dochází k úniku paprsků pryč z jádra.

Obr. 5. Totální odraz světelného paprsku po překročení mezního úhlu