Základy fyzikální chemie pro VOŠ

5.4

Druhá věta termodynamiky

První věta termodynamiky vycházela ze zákona o zachování energie a zabývala se kvantitativním vztahem mezi teplem, prací a vnitřní energií. Druhá věta termodynamiky se týká směřování samovolných přeměn v přírodě a možností využití samovolného přechodu tepla, přeměnou v práci.

5.4.1

Vratné a nevratné děje

Z běžného života známe samovolné (spontánní) děje, které probíhají určitým směrem. Předmět puštěný z výšky vždy padá dolů k zemi, nikoliv nahoru; teplejší těleso předává teplo chladnějšímu a ne naopak, plyn snadno přejde z prostoru o vyšším tlaku do místa o nižším tlaku, opačně nikoliv; kostka cukru se v čaji rozpustí, ale nelze vytáhnout rozpuštěný cukr z kávy atd. Všechny tyto děje a mnohé další probíhají jednosměrně a nevratně (ireverzibilně). Směřují vždy k dosažení rovnovážného stavu, např. k vyrovnání teplot, tlaků, koncentrací apod.

K vrácení do předcházejícího stavu je potřeba vykonat práci, např. zvednout předmět, stlačit plyn, ochladit těleso.

Kromě nevratných pochodů existují i vratné (reverzibilní), které nastávají tehdy, pokud se v jakémkoliv okamžiku provede nekonečně malá změna vnějších podmínek. Může se jednat o velmi malý posun pístu jedním směrem a jeho náprava směrem opačným – viz probraná ukázka zatěžovaného pístu zrníčky písku.

Druhý termodynamický zákon je opět postulátem (axiomem), tzn. že je založen na dlouhodobé lidské zkušenosti ověřené časem. Formulace druhého termodynamického principu vychází ze závěrů pozorování samovolných přírodních procesů. Nejčastějšími formulacemi jsou:

Definice

Teplo nemůže samovolně přecházet z tělesa chladnějšího na teplejší. (Clausius)

Není možné konat periodicky práci na úkor tepla odebíraného tělesu, majícímu všude stejnou teplotu, bez současného převodu části tepla na těleso chladnější. (Kelvin)

Z druhé formulace plyne, že nelze sestrojit perpetuum mobile druhého druhu.

Poznámka

Perpetuum mobile druhého druhu je ideální stroj, který dokáže přeměňovat odebírané teplo z jedné lázně (teplota je v celé lázni stejná) a přeměňovat toto teplo beze zbytku na práci.

Ve skutečnosti ale cyklicky pracující tepelný stroj nelze sestrojit tak, aby jen odebírané teplo přeměňoval na práci. Vždy dojde i k předání tepla chladnějšímu tělesu.

K objevu druhého termodynamického principu vedly snahy o analýzu účinnosti tepelných strojů.

5.4.2

Tepelné stroje, Carnotův cyklus

Do skupiny tepelných strojů patří parní stroj a spalovací motory. Tepelné stroje využívají přeměnu tepla na práci, pracují cyklicky (vracejí se neustále do výchozího stavu). Tepelný stroj musí pracovat alespoň se dvěma tepelnými lázněmi (zásobníky) rozdílné teploty.

Na obrázku č. 34 je zobrazeno schéma tepelného stroje. Horní zásobník (ohřívač) má teplotu T₂ a dolní zásobník (chladič) má teplotu T₁. Uprostřed je tepelný stroj, který přijímá teplo Q₂ z ohřívače a přeměňuje část tohoto tepla na práci W a část tepla Q₁ předává chladiči.

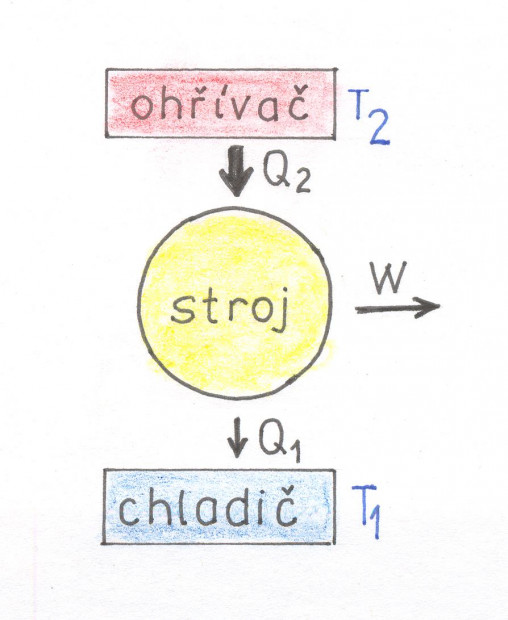
Obr. 34. Tepelný stroj.

Práci tepelného stroje vysvětluje Carnotův teoretický stroj. Náplní stroje je ideální plyn. Stroj pracuje cyklicky. Jeden pracovní cyklus se skládá ze čtyř pracovních částí. Ve dvou částech dochází k expanzi – izotermické a adiabatické – a pak ve dvou částech dochází ke kompresi – izotermické a adiabatické. Podmínkou cyklu je, že všechny pochody musí probíhat vratně.

Při expanzích plyn koná práci, posouvá píst a při kompresích stroj přijímá práci k vrácení pístu do původní polohy. Během činnosti stroj odebírá teplo z ohřívače a předává teplo chladiči. Zásobníky (ohřívač a chladič) mají tak velkou kapacitu, že se při odebírání a dodávání tepla jejich teploty nemění.

Obrázek č. 35 představuje schéma Carnotova cyklu. Z bodu 1 → 2 probíhá izotermická expanze, 2 → 3 adiabatická expanze, 3 → 4 izotermická komprese a 4 → 1 adiabatická komprese.

Vyšrafovaná plocha představuje pracovní zisk v jednom čtyřdobém cyklu tepleného stroje. Zisk je rozdíl práce strojem vykonané při expanzi plynu a práce stroji dodané při kompresi.

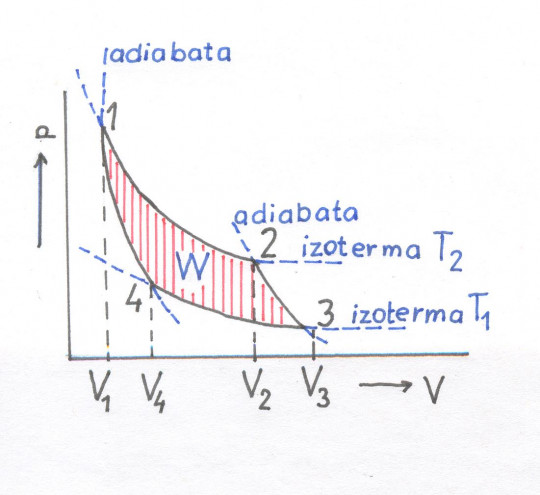
Obr. 35. Carnotův cyklus

Jednotlivé pochody: z bodu 1 → 2 probíhá izotermická expanze, 2 → 3 adiabatická expanze, 3 → 4 izotermická komprese a 4 → 1 adiabatická komprese.

Na dalších obrázcích č. 36–39 jsou jednotlivé pochody znázorněné pomocí grafu a pístu ve válci.

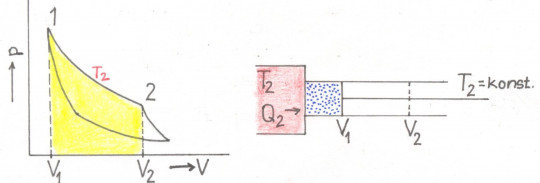
36. Carnotův cyklus – izotermická expanze (1. část); V1, p1, T2 → V2, p2,T2

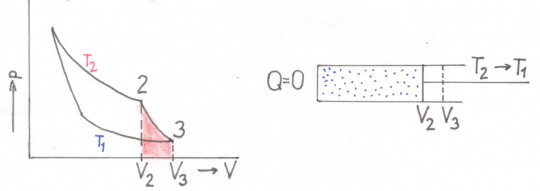
Obr. 36. Carnotův cyklus – izotermická expanze (1. část); V₁, p₁, T₂ → V₂, p₂,T₂

37. Carnotův cyklus – adiabatická expanze (2. část); V2, p2, T2 → V3, p3,T1

Obr. 37. Carnotův cyklus – adiabatická expanze (2. část); V₂, p₂, T₂ → V₃, p₃,T₁

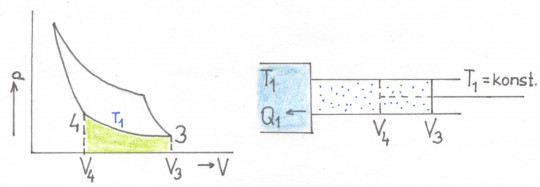
38. Carnotův cyklus – izotermická komprese (3. část); V3, p3, T1 → V4, p4,T1

Obr. 38. Carnotův cyklus – izotermická komprese (3. část); V₃, p₃, T₁ → V₄, p₄,T₁

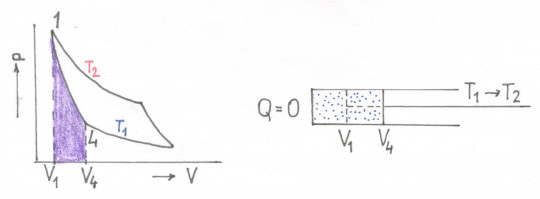
39. Carnotův cyklus – adiabatická komprese (4. část); V4, p4, T1 → V1, p1,T2

Obr. 39. Carnotův cyklus – adiabatická komprese (4. část); V₄, p₄, T₁ → V₁, p₁,T₂

Nyní k jednotlivým fázím Carnotova cyklu:

izotermická expanze (1 → 2): Plyn uzavřený ve válci byl stlačený na výchozí objem V₁, je pod tlakem p₁ a jeho počáteční teplota je T₂. Nastane izotermická expanze, při níž se objem plynu zvětší na V₂ a tlak poklesne na p₂. Počáteční teplota T₂ je teplota ohřívače, s nímž je válec spojen. Plyn odčerpá teplo Q₂ a převede jej na práci W₁(plyn koná práci, protoznaménko minus):
$Q_{2} = - W_{1} = n \cdot R \cdot T_{2} \cdot l n \frac{V_{2}}{V_{1}}$

adiabatická expanze (2 → 3): Plyn v tepelně izolovaném válci (Q = 0) zvětší svůj objem na V₃, dojde ke snížení tlaku na hodnotu p₃ a ochladí se na teplotu T₁. Plyn koná práci na úkor své vnitřní energie:
$- W_{2} = ∆ U = n \cdot C_{V} \cdot ∆ T = n \cdot C_{V} \cdot (T_{1} - T_{2})$

izotermická komprese (3 → 4): Pístem ve válci je plyn izotermicky při teplotě T₁ stlačován. Objem plynu se zmenší z V₃ na V₄ a tlak vzroste z p₃ na p₄. Plyn předá teplo Q₁ chladiči. Práce vynaložená k posunutí pístu do bodu 3 je dána vztahem (systému je práce dodaná, proto znaménko plus):
$- Q_{1} = + W_{3} = n \cdot R \cdot T_{1} \cdot l n \frac{V_{4}}{V_{3}}$

adiabatická komprese (4 → 1): Plyn se převede adiabatickou kompresí do bodu 1 tj. do počátečního bodu cyklu pomocí dodané práce a teplota vzroste na teplotu T₂:
${+ W}_{4} = n \cdot C_{V} \cdot (T_{2} - T_{1})$

Vykonanou práci Carnotova cyklu lze graficky vyjádřit jako obsah vyšrafované plochy ohraničené body 1,2,3,4. Matematicky se celková práce rovná součtu jednotlivých příspěvků:

W = W_{1} + W_{2} + W_{3} + W_{4}

Protože podle úmluvy platí, že vykonaná práce (–) a dodaná (+), pak přesnější zápis bude:

- W = (- W_{1}) + ({- W}_{2}) {+ W}_{3} {+ W}_{4}

Práci odvedenou strojem lze po dosazení a úpravách vyjádřit rovnicí:

- W = n R (T_{2} - T_{1}) l n \frac{V_{2}}{V_{1}}

Poznámka

Matematické odvození práce stroje:

- W = n R (T_{2} - T_{1}) l n \frac{V_{2}}{V_{1}}

Úpravy:

- W = (- W_{1}) + ({- W}_{2}) {+ W}_{3} {+ W}_{4}

po dosazení:

- W = n \cdot R \cdot T_{2} \cdot l n \frac{V_{2}}{V_{1}} + n \cdot C_{V} \cdot (T_{1} - T_{2}) + n \cdot R \cdot T_{1} \cdot l n \frac{V_{4}}{V_{3}} + n \cdot C_{V} \cdot (T_{2} - T_{1})

druhý a čtvrtý člen lze od sebe odečíst, pak:

- W = n \cdot R \cdot T_{2} \cdot l n \frac{V_{2}}{V_{1}} + n \cdot R \cdot T_{1} \cdot l n \frac{V_{4}}{V_{3}}

pro T, V platí Poissonovy rovnice (2 → 3) a (4 → 1):

T_{2} \cdot {(V_{2})}^{κ - 1} = T_{1} \cdot {(V_{3})}^{κ - 1}

{T_{2} \cdot {(V_{1})}^{κ - 1} = T}_{1} \cdot {(V_{4})}^{κ - 1}

podělením rovnic a odmocněním: $\frac{V_{2}}{V_{1}} = \frac{V_{3}}{V_{4}}$

protože dosazujeme $z a o b r á c e n ý z l o m e k \frac{V_{3}}{V_{4}}$ , je nutné 2. člen odečíst:

- W = n \cdot R \cdot T_{2} \cdot l n \frac{V_{2}}{V_{1}} - n \cdot R \cdot T_{1} \cdot l n \frac{V_{2}}{V_{1}}

pro strojem odevzdanou práci dostaneme: $- W = n \cdot R \cdot l n \frac{V_{2}}{V_{1}} (T_{2} - T_{1})$

Účinnost stroje:

η = \frac{o d e v z d a n á p r á c e}{d o d a n é t e p l o} = \frac{- W}{Q_{2}} = \frac{n R (T_{2} - T_{1}) l n \frac{V_{2}}{V_{1}}}{n \cdot R \cdot T_{2} \cdot l n \frac{V_{2}}{V_{1}}} = \frac{T_{2} - T_{1}}{T_{2}}

η = \frac{T_{2} - T_{1}}{T_{2}}

Definice

Účinnost Carnotova stroje nezávisí na druhu použitého plynu, ale pouze na teplotách ohřívače a chladiče. Carnotův stroj nemůže pracovat se stoprocentní účinností, protože vždy část tepla musí vrátit chladnější lázni.

Video 2. Carnotův cyklus

Poznámka

Všechny části v ideálním Carnotově cyklu jsou vratné. Obrácením pochodů Carnotova stroje bude děj probíhat 1→4→3→2→1. Tam, kde probíhala expanze, probíhá komprese a naopak.

(1→4) adiabatická expanze: teplota poklesne z T₂ na T₁, plyn koná práci,

(4→3) izotermická expanze: teplota T₁ je konstantní, aby při expanzi nedocházelo k dalšímu poklesu teploty, odebere plyn teplo (Q₁ ) chladiči a koná expanzí práci,

(3→2) adiabatická komprese: plyn je stlačen, a proto teplota vzroste z T₁ na T₂,

(2→1) izotermická komprese: plyn je stlačen za konstantní teploty, a aby teplota nevzrostla, předá teplo (Q₂) ohřívači.

Podíváme-li se na graf, vidíme, že tentokrát práci nezískáme, naopak ji musíme stroji k činnosti dodat. Popsané pochody vysvětlují činnost chladicího stroje. Z popsaných pochodů lze vidět, že účelem chladicích zařízení (chladničky, mrazničky, klimatizace) je ochlazovat studený zásobník (chladič). Kromě ochlazování studeného zásobníku dochází v cyklu i k ohřívání teplého zásobníku (ohřívače). Tuto skutečnost využívá tepelné čerpadlo.

5.4.3

Entropie

Další stavovou veličinou je entropie. Její název pochází z řečtiny („en trepein“ = udávat směr). Označuje se S a jednotky jsou J ∙ K^-1. Entropii lze matematicky vyjádřit pomocí jejího diferenciální rovnice:

d S = \frac{{d Q}_{r e v}}{T}

Q_rev ... množství tepla přijaté soustavou při nekonečně malé reverzibilní (= vratné) změně jejího stavu,

T ... termodynamická teplota soustavy.

Pro nevratný (ireverzibilní) děj platí:

d S > \frac{{d Q}_{i r}}{T}

Pro adiabatický děj (

d Q

= 0); po dosazení pro vratný i nevratný děj:

d S \geq 0

Dané vztahy mají povahu axiomů.

Velikost entropie nezávisí na cestě, ale jen na počátečním a konečném stavu, proto entropie kruhového cyklu je rovna nule.

Probíhá-li děj v izolované soustavě, pak entropie roste až po dosažení maximální hodnoty, kdy dojde k ustavení rovnováhy.

V současnosti je entropie chápána jako veličina udávající míru neuspořádanosti nebo chaosu systému. Uspořádané stavy jsou méně pravděpodobné než stavy neuspořádané. Při samovolném přechodu soustavy do pravděpodobnějšího stavu dochází k nárůstu entropie. Systém s vysokou entropií je neuspořádaný, s nízkou entropií uspořádaný. Příkladem termodynamického systému s nízkou entropií jsou např. dva plyny oddělené přepážkou. Po odstranění přepážky dojde ke smíšení plynů a ke zvýšení entropie. Jiným příkladem je zvýšení entropie při odpaření kapalné látky. Její molekuly měly v kapalině menší chaotický pohyb než molekuly vypařené plynné látky.

Také v běžném každodenním životě lze najít pár příkladů: polička s knihami seřazenými podle určitého klíče, pořádek na pracovním stole, lidé využívající efektivně svůj čas, mající své aktivity zorganizované, pro každou věc mají své místo – to jsou ukázky nízkých entropií. Naopak vysokou entropii najdeme u zmatkařů věčně něco hledajících, obdobně u nepořádku na pracovním stole nebo v policích s knihami apod.

Definice

Entropie je mírou chaosu (neuspořádanosti) soustavy.

Název entropie je odvozen od udávání směru. Entropie určuje směr plynutí času. Díváme-li se na film, poznáme, kdy běží pozpátku (ze střepů rozbité vázy vzniká na stole váza celá, rozlitá voda z podlahy se vrátí zpátky do sklenice, ...). Čas ale nelze obrátit. Dřevo shořelé v krbu na popel již nelze ani pochytáním kouře a spojením s popelem přeměnit ve dřevo. Žádná situace se nestane dvakrát úplně stejně. Dřevo hořící příště v krbu je jiné, my jsme trochu jiní, máme jinou náladu, starosti, zkušenosti (minimálně s předchozím topením v krbu)...

Entropii lze využít k popisu tepelných strojů. Použitím místo grafického znázornění pomocí souřadnic tlak – objem (p – V) lze využít souřadnice teplota – entropie (T – S). Získáme tím plochu obdélníku, v němž horizontální čáry odpovídají izotermám a vertikální adiabatám (izoentropám).

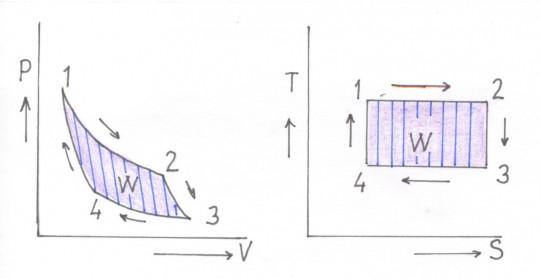
Obr. 40. Diagramy pro Carnotův cyklus

Poznámka

Při vratném adiabatickém ději se entropie nemění. Takovým dějům říkáme izoentropické.

Také v přírodě si můžeme všimnout nevratných procesů spojených s nárůstem entropie – eroze hornin, sopečné výbuchy, hurikány... Také člověk přispívá svou činností a znečištěním.

Podobně jako byla v prvním termodynamickém zákoně důležitá vnitřní energie, tak ve druhém je významná entropie. Cílem druhého termodynamického zákona je získání užitečné práce z termodynamické soustavy. Aby soustava konala práci, musí docházet k samovolným procesům (viz např. expanze plynu v Carnotově cyklu). Spontánní (samovolné) děje probíhají ve směru růstu entropie až po dosažení maximální hodnoty, kdy dojde k ustavení rovnováhy.

Definice

Entropie je termodynamickou funkcí charakterizující stav a možnost změny stavu hmotných soustav nebo také pravděpodobnost možných stavů daného systému nebo soustavy.

5.4.4

Gibbsova energie

Gibbsova energie (dřívější název volná entalpie) je extenzivní stavová veličina. Značí se G a její jednotkou je J (joule). Popisuje chemické děje probíhající za konstantního tlaku, teploty a látkového množství.

Gibbsovu energii lze vyjádřit pomocí entalpie (H), entropie (S) a termodynamické teploty (T):

G = H - T \cdot S

∆ G = ∆ H - T \cdot ∆ S

G = U - T \cdot S + p \cdot V

Obsah Gibbsovy energie se při chemických reakcích mění. Změnu lze zapsat jako rozdíl ΔG mezi konečným stavem G₂ a počátečním stavem G₁ soustavy:

∆ G = G_{2} - G_{1}

Z hlediska rozdílů Gibbsovy energie rozlišujeme tři případy:

G₂ < G₁, ... ΔG < 0...... exergonický děj (energie se uvolňuje)

G₂ > G₁, ... ΔG > 0 ...... endergonický děj (energie se spotřebovává)

G₂ = G₁, ... ΔG = 0 ...... systém je v rovnováze (energie se ani nedodává, ani nespotřebovává)

Exergonické děje jsou typické pro katabolické děje v živém organismu. Při dějích dochází k rozkladu složitějších sloučenin na jednodušší a uvolňuje se při nich energie. Získanou energii může organismus použít např. k syntéze ATP.

Naopak endergonické děje se využívají při anabolických (syntetizujících) dějích. K tvorbě složitějších sloučenin spotřebovávají energii, která je jim dodávána prostřednictvím makroergické sloučeniny ATP.