Základy fyzikální chemie pro VOŠ

5.2

První věta termodynamiky

5.2.1

Objemová práce

Problematika práce a tepla je klíčem k první termodynamické větě. Práce a teplo jsou dvě různé formy výměny energie mezi soustavou a okolím.

Objemová práce W plynu nastane při změně objemu z hodnoty V₁ na hodnotu V₂. K odvození použijeme představu válce, ve kterém je stlačován plyn.

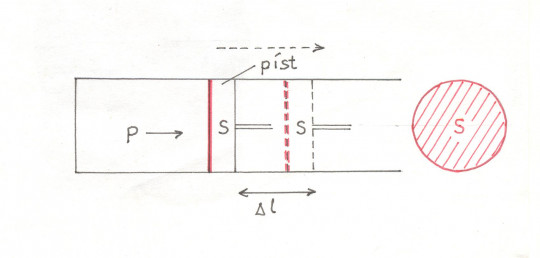
Obr. 24. Objemová práce – expanze plynu po stlačení pístem ve válci

Na obrázku je nakreslen válec s plynem. Plyn je stlačován pomocí pístu, dochází ke kompresi plynu. Po uvolnění pístu dochází k expanzi plynu. Plyn koná objemovou práci W. Plyn působí na plochu pístu S tlakem p. Celková síla působící na píst je F = p ∙ S. Píst se posune (směr posunu pístu je označen šipkou čárkovaně) o dráhový rozdíl ∆l:

W = - F \cdot Δ l = - p \cdot S \cdot Δ l = - p \cdot Δ V

Pokud je třeba vyjádřit, zda soustava přijala nebo vydala práci, pak konaná (vydaná) práce se značí záporným znaménkem a přijatá kladným.

5.2.2

Vnitřní energie

U termodynamického systému rozlišujeme vnější a vnitřní energii. Vnější energií myslíme u soustavy jako celku (např. tělesa) energii kinetickou (tj. pohybovou) a energii potenciální (tj. polohovou), kterou má každé těleso nacházející se v potenciálovém poli určité síly (např. v tíhovém poli).

V termodynamice nás ale zajímá vnitřní energie. Jedná se o souhrn různých energií částic a atomů v soustavě. Zahrnuje energii tepelnou (kinetickou energii elementárních částic), chemickou (vazebnou energii atomů v molekulách), jadernou (vazebnou energii nukleonů v jádrech atomů), polohovou (projevující se např. jako stlačitelnost/pružnost), popř. magnetickou, elektrickou. Vnitřní energii nelze v určitém okamžiku změřit. Je možné změřit pouze změnu vnitřní energie

Δ U

, přechází-li soustava ze stavu A do stavu B.

∆ U = U_{B} - U_{A}

Podle prvního termodynamického zákona platí:

∆ U = Q + W

Definice

První termodynamický zákon: Změna vnitřní energie soustavy ΔU se rovná součtu tepla Q a práce W vyměněné s okolím.

Jeden ze základních zákonů ve fyzice je zákon o zachování energie, který říká, že energie nemůže z ničeho vzniknout a také že ji nelze zničit, pouze ji lze přeměnit na jiný druh energie.

První věta termodynamiky je jeho specifickou formulací, podle níž teplo dodané systému může být přeměněno na práci nebo se spotřebovat na zvýšení obsahu vnitřní energie, popř. obojí současně.

Pozor:

Teplo a práce vyměněné mezi systémem a okolím při přechodu systému ze stavu A do stavu B závisejí nejen na uvedeném počátečním a konečném stavu, ale také na zvolené cestě mezi stavem A a B.

Součet tepla a práce je dán rozdílem

∆ U = U_{B} - U_{A}

, tj. závisí pouze na počátečním a konečném stavu.

Poznámka

Matematická formulace I. věty termodynamické pro uzavřený systém zapsaná v diferenciálním stavu:

dU=đQ + đW

Symboly d a đ velmi zjednodušeně znamenají infinitezimálně malé změny. Písmeno d značí úplný diferenciál. Integrál úplného diferenciálu nezávisí na cestě. Symbol đ představuje neúplný diferenciál, jehož integrál závisí na cestě.

Integrál se v matematice používá např. k výpočtu plochy.

[infinitezimální = nekonečně malý, např. číslo]

Příklad

Příklad 5.1

Uzavřenému systému byla dodána energie 1200 J ve formě tepla. Jak se změnila vnitřní energie systému, jestliže vykonal práci 500 J?

Zobrazit řešení

Skrýt řešení

Řešení

ze zadání:

ΔU = ?

Q = 1200 J

W =

-

500 J (znaménko minus značí vykonanou práci)

výpočet:

∆ U = Q + W = 1200 - 500 = 700 J

Změna vnitřní energie je 700 J.

Příklad

Příklad 5.2

Soustava vykonala práci 58 kJ. Její vnitřní energie vzrostla o 12 500 J. Kolik tepla soustava přijala nebo odevzdala?

Zobrazit řešení

Skrýt řešení

Řešení

Q = + 70 500 J (+ značí soustavou přijaté, soustavě dodané)

Soustava přijala 70,5 kJ tepla.

5.2.3

Důsledky 1. zákona termodynamiky

Jestliže pro 1. zákon termodynamiky platí:

∆ U = Q + W

pak pro konanou práci musí platit:

- W = - ∆ U + Q

Z rovnice je vidět, že soustava může konat práci na úkor úbytku vnitřní energie nebo na úkor dodaného tepla. Práce tedy nevzniká z ničeho.

Z prvního zákona termodynamiky vyplývá, že nelze sestrojit perpetuum mobile prvního druhu, tj. stroje, který by konal cyklicky práci, a přitom by nepřijímal z okolí energii. Stroj by se měl podle představy rozeběhnout nějakým počátečním impulsem a pak už by měl nepřetržitě běžet, aniž by mu byl dodáván jakýkoliv druh energie. Jinak řečeno, konal by užitečnou práci z ničeho.

První zákon termodynamiky ale nezakazuje přeměnit tepelnému stroji veškeré teplo v práci. Při matematickém odvozování nastane u cyklického děje, kde

∆ U = (U_{B} - U_{A}) + (U_{A} - U_{B}) = 0

. V kapitole o druhém termodynamickém zákoně se dozvíme, že to možné není.

Poznámka

Historické návrhy perpetua mobile často spočívaly v nedůsledném rozmyšlení rozložení sil v klasické mechanice. Jiné návrhy z této skupiny používají magnety jako nevyčerpatelný zdroj energie a vyhýbají se vzájemnému dotyku jednotlivých pohyblivých částí. Takové stroje často dokážou pracovat velmi dlouho. Problém je v tom, že ve skutečnosti nejsou schopny poskytnout žádnou skutečnou mechanickou práci k pohonu nějakého vnějšího zařízení. [57]

5.2.4

Změny vnitřní energie u jednotlivých dějů:

5.2.4.1

Izotermický děj, t = konst.

Vnitřní energie ideálního plynu je rovna energii pohybujících se molekul, která je funkcí teploty. Proto při konstantní teplotě bude změna vnitřní energie rovna nule.

Po dosazení:

∆ U = Q + W = 0 t a k ž e Q = - W n e b o - Q = W

Z matematického odvození plyne, že přijaté teplo se rovná vykonané práci a naopak odevzdané teplo se rovná přijaté práci.

Velikost práce závisí na cestě, proto budeme rozlišovat vratné a nevratné provedení expanze a komprese.

Izotermická expanze

1. Nevratné provedení – změna proběhne náhle, tlak klesne náhle (skokem) na hodnotu p₂. Průběh je znázorněn na obr. 25. Ve válci je plyn stlačovaný pístem. Píst je zatížen velkým závažím. Náhle závaží odstraníme. Dojde k prudkému poklesu tlaku a plyn se začne rozpínat z původního objemu V₁ na V₂. Práci, kterou soustava vykoná, znázorňuje v grafu vybarvený obdélník. Matematicky lze práci vyjádřit rovnicí:
  $W = - p_{2} \cdot ∆ V = - p_{2} \cdot (V_{2} - V_{1})$
  V₂ > V₁, práce bude se znaménkem minus tzn., že soustava práci vykoná.

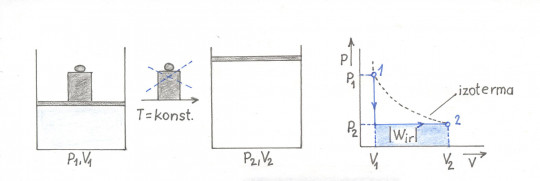
Obr. 25. Izotermická expanze – nevratná

1. Vratné provedení – expanzní změny probíhají po velmi malých krůčcích. Pokud provedeme velmi malou opačnou změnu, tak proces změn zastavíme a dalšími malými změnami můžeme dokonce pomalu vracet do původního stavu. Situaci znázorňuje obr. 26. Píst je tentokrát zatížen pomyslným závažím z písku. Ze závaží odstraňujeme písek – zrníčko po zrníčku. Tlak po velice malých úbytcích klesá, v grafu jsou úbytky zakresleny schůdky pod izotermou. Schůdky jsou velice maličké, při pozorování z větší dálky splývají v jednu křivku (viz pravý graf). Vykonaná práce je v grafu znázorněna plochou pod křivkou. Pro zjištění velikosti ploch pod křivkou se využívá výpočtů za použití integrálů. Řešením se do rovnice dostává přirozený logaritmus podílu. Pro odvození matematického vztahu vykonané práce využijeme i stavovou rovnici ideálního plynu a dostáváme vztah:
  $W = - n R T \cdot \ln \frac{V_{2}}{V_{1}} = - n R T \cdot \ln \frac{p_{1}}{p_{2}}$

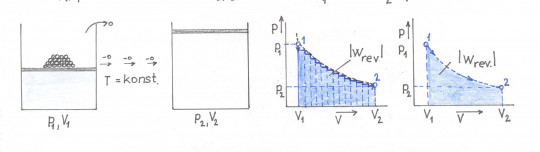
Obr. 26. Izotermická expanze – vratná

Izotermická komprese

1. nevratné provedení – ke kompresi dojde náhle skokovým zvýšením tlaku. To si lze představit náhlým umístěním velkého závaží na píst, který stlačuje plyn. Objem plynu se bude zmenšovat. Graficky práci znázorňuje v obr. 27 větší obdélník. Práci lze vypočítat podle vztahu:
  $W = - p_{2} \cdot ∆ V = - p_{2} \cdot (V_{2} - V_{1})$
  V₂< V₁, práce bude se znaménkem plus – tzn., že soustavě je třeba práci dodat.

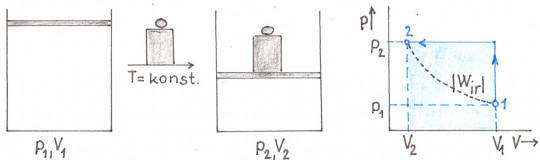
Obr. 27. Izotermická komprese – nevratná

1. Vratné provedení – kompresní změny probíhají velmi pomalu. Na obrázku 28 změny nastávají postupným přidáváním závaží. Zde jsou pro představu velmi malých změn závažím zrnka písku. Pro grafické vyjádření velikosti práce dostáváme opět plochu pod křivkou. Matematicky:
  V₂ < V₁, práce bude se znaménkem plus – tzn., že soustavě je třeba práci dodat.

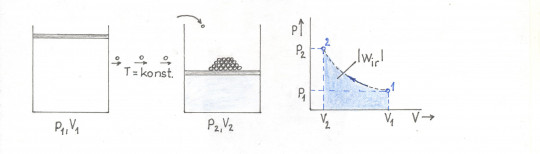
Obr. 28. Izotermická komprese – vratná

Příklad

Příklad 5.3

2,5 molu ideálního plynu se při teplotě 20 °C izotermicky rozpíná z objemu 30 litrů na objem 58 litrů. Jakou práci soustava vykoná při nevratném a vratném průběhu děje?

Zobrazit řešení

Skrýt řešení

Řešení

ze zadání:

n = 2,5 mol

t =20 °C; T = 273 + 20 = 293 K

V₁= 30 l = 0,03 m³ =30∙10^-3 m³

V₂= 58 l = 0,058 m³

W_ire = ?

W_rev = ?

výpočet:

nevratná/ireverzibilní expanze

W_{I r e} = - p_{2} \cdot (V_{2} - V_{1}) = - p_{2} \cdot ∆ V

p₂= ?

ze stavové rovnice:

p \cdot V = n \cdot R \cdot T

p_{2} = \frac{n \cdot R \cdot T}{V_{2}} = \frac{2,5 \cdot 8,314 \cdot 293}{0,058} = 105000,0862 P a \dot{=} 105 k P a

W_{i r e} = - 105 \cdot 10^{3} \cdot (58 - 30) \cdot 10^{- 3} = - 2940 J \dot{=} - 2,94 k J

vratná/reverzibilní expanze

W_{r e v} = - n \cdot R \cdot T \cdot l n \frac{V_{2}}{V_{1}} = - 2,5 \cdot 8,314 \cdot 293 \cdot l n \frac{58 \cdot 10^{- 3}}{30 \cdot 10^{- 3}} = - 4014,809 J \dot{=} - 4,014 k J

Soustava vykoná při nevratné expanzi práci 2,94 kJ a při vratné 4,01 kJ.

Příklad

Příklad 5.4

5 molů ideálního plynu za izotermních podmínek při teplotě 300 K změnilo svůj objem. Původní tlak plynu byl 0,08 MPa a konečný tlak 170,4 kPa. Došlo k expanzi nebo ke kompresi plynu? Vypočítej práci konanou/dodanou při nevratném ději a při vratném ději.

Zobrazit řešení

Skrýt řešení

Řešení

ze zadání:

n = 5 mol

T = 300 K

p₁= 0,08 MPa = 0,08 ∙ 10⁶ Pa = 80 000 = 80 kPa

p₂= 170,4 kPa = 170,4 ∙ 10³ Pa = 170 400 Pa

výpočet:

p_2 >p₁=> jedná se o kompresi plynu

V_{1} = \frac{n \cdot R \cdot T}{p_{1}} = \frac{5 \cdot 8,314 \cdot 300}{80 \cdot 10^{3}} = 0,1558875 m^{3} \dot{=} 0,1559 m^{3}

V_{2} = \frac{n \cdot R \cdot T}{p_{2}} = \frac{5 \cdot 8,314 \cdot 300}{170,4 \cdot 10^{3}} = 0,073186619 m^{3} \dot{=} 0,0732 m^{3}

nevratná:

W = - p_{2} \cdot ∆ V = - 170400 \cdot (0,0732 - 0,1559) = - 170400 \cdot (- 0,0827) = 14092,08 J \dot{=} 14,09 k J

Práce vyšla kladně – jedná se o dodanou práci plynu.

Práce dodaná při nevratné kompresi je 14,09 kJ.

vratná:

W = - n R T \cdot \ln \frac{V_{2}}{V_{1}} = - 5 \cdot 8,314 \cdot 300 \cdot \ln \frac{0,0732}{0,1559} = - 12471 \cdot (- 0,756019) = 9428,3 J \dot{=} 9,43 k J

W = - n R T \cdot \ln \frac{p_{1}}{p_{2}} = - 5 \cdot 8,314 \cdot 300 \cdot l n \frac{80 \cdot 10^{3}}{170,4 \cdot 10^{3}} \dot{=} 9,43 k J

Práce dodaná při vratné kompresi je 9,43 kJ. Ve srovnání s nevratnou kompresí je menší.

5.2.4.2

Izochorický děj, V = konst.

Jestliže se nemění objem (ΔV = 0), tak plyn nekoná práci. W = 0. Po dosazení do 1. termodynamické věty, dostáváme:

∆ U = Q + 0

∆ U = Q

Definice

Teplo Q vyměňované mezi soustavou a okolím při izochorickém ději se rovná změně vnitřní energie ΔU.

Znamená to, že teplo dodané soustavě za konstantního objemu se využije k jejímu ohřevu.

5.2.4.3

Izobarický děj, p = konst.

Do vztahu pro 1. termodynamickou větu ΔU = Q + W dosadíme za práci W vztah pro objemovou práci – p ∙ ΔV. Dále pokračujeme odvozováním:

∆ U = Q - p . ∆ V

(U_{2} - U_{1}) = Q - p \cdot (V_{2} - V_{1})

U_{2} - U_{1} = Q - p \cdot V_{2} + p \cdot V_{1}

Q = (U_{2} + p \cdot V_{2}) - (U_{1} + p \cdot V_{1})

H = U + p V

Q = H_{2} - H_{1} = ∆ H

H ... entalpie, extenzivní stavová funkce; lze měřit pouze změnu entalpie.

5.2.4.4

Entalpie

Definice

Teplo Q vyměněné mezi soustavou a okolím při izobarickém ději se rovná změně entalpie ΔH. Jednotkou entalpie je joule (J) [džaul].

Může nastat:

ΔH > 0, pak soustava při chemické reakci teplo přijímá ... endotermická (endotermní) reakce

ΔH < 0, pak soustava při chemické reakci teplo odevzdává, uvolňuje ... exotermická (exotermní) reakce

5.2.4.5

Adiabatický děj

Adiabatický děj probíhá v tepelně izolovaných soustavách. Při adiabatickém ději nedochází k výměně tepla mezi systémem a okolím.

Q = 0

Po dosazení do 1. termodynamické věty:

∆ U = Q + W = 0 + W

∆ U = W

Adiabaticky přijatou prací (při adiabatické kompresi) soustava zvyšuje svou vnitřní energii a ohřívá se. Pokud koná soustava adiabatickou práci (při expanzi), koná ji na úkor své vnitřní energie, takže se ochlazuje.

V případě ideálního plynu platí:

W = ∆ U = n \cdot C_{v} \cdot ∆ T

C_v ...izochorická molární tepelná kapacita

Adiabaticky izolovaný ideální plyn se při expanzi ochlazuje (ΔT < 0) a koná práci (W< 0) na úkor své vnitřní energie (ΔU < 0, C_v> 0). Při adiabatické kompresi je tomu opačně.

Probíhá-li adiabatická expanze nebo komprese ideálního plynu reverzibilně, platí pro jeho tlak a objem Poissonovy rovnice.

p \cdot V^{κ} = k o n s t .

T \cdot V^{κ - 1} = k o n s t .

T \cdot p^{(1 - κ) / κ} = k o n s t .

κ ... [čti kapa] se nazývá Poissonova konstanta

κ = C_{p} / C_{v} = c_{p} / c_{v}

C_p ...izobarická molární tepelná kapacita

c_p ...izobarická měrná tepelná kapacita

c_v ...izochorická měrná tepelná kapacita

Pro jednoatomové ideální plyny je hodnota

κ \dot{=} 1,67

, pro dvouatomové molekuly

κ \dot{=} 1,40

Pamatujte si, že Poissonovy rovnice platí pokud:

se jedná o adiabatický vratný děj,

počítáme s ideálním plynem,

tepelné kapacity nezávisí na teplotě,

se koná jen objemová práce.

Není-li jediná z podmínek splněna, Poissonovy rovnice neplatí.

5.2.5

Teplo

V kapitole 5.2 prvního termodynamického zákona se mluví o teplu. Teplo je možné kalorimetricky změřit. Pro výpočty je třeba znát také tepelnou kapacitu látek.

5.2.5.1

Tepelná kapacita

Každá látka potřebuje k ohřátí o určitou teplotu jiné množství tepla. Proto byla zavedena tepelná kapacita. Značíme ji K.

Definice

Tepelná kapacita je fyzikální veličina vyjadřující množství tepla potřebného k ohřátí soustavy o 1 K (Kelvin), respektive o 1 °C, neboť ΔT = Δt.

K = \frac{Q}{∆ T} [J \cdot K^{- 1}]

Q ... teplo, které soustava přijala při ohřátí o

∆ T

∆ T \dots

teplotní interval vyjadřující, o kolik se zvýšila teplota:

∆ T = T_{2} - T_{1}

Tepelná kapacita má jednotku J ∙ K^-1. V uvedeném matematickém tvaru odpovídá celé soustavě. V praxi se používají tabelované hodnoty, které jsou vztažené na jednotku hmotnosti nebo na 1 mol.

Definice

Specifická (měrná) tepelná kapacita c udává množství tepla potřebného k ohřátí 1 kg látky o 1 K.

c = \frac{K}{m} [J \cdot K^{- 1} \cdot {k g}^{- 1}]

Definice

Molární tepelná kapacita C udává množství tepla potřebného k ohřátí 1 molu látky o 1K.

C = \frac{K}{n} [J \cdot K^{- 1} \cdot {m o l}^{- 1}]

Poznámka

Hodnoty tepelných kapacit v tabulkách bývají označeny indexy p nebo V. Znamenají, že hodnoty byly stanoveny při konstantním tlaku nebo objemu.

Tabulka 5. Tepelné kapacity vybraných látek

látka	c [J ∙ K^-1∙ kg^-1]
voda	4180
led	2090
měď	383
olovo	129
ethanol	2430
beton	800-1100

Zkusme se zamyslet nad hodnotami v tabulce:

Vyšší hodnoty c značí podle definice potřebu dodání většího množství tepla k ohřátí o 1 °C nebo 1 K.

Led má poloviční tepelnou kapacitu v porovnání s vodou. Proto je k ohřátí vody o 1°C potřeba dvojnásobné množství tepla oproti ohřátí ledu o 1 °C. (Může jít o libovolný 1°C, např. ohřev ledu z -10 °C na -9 °C a vody z 62 °C na 63 °C. Zde samozřejmě uvažujeme jen o teplotách, kdy je led ledem a voda vodou, neuvažujeme o skupenských přeměnách.)

Beton má 4x – 5x menší hodnotu než voda, a tak se nelze divit, že v létě není až tak nesnadné jej v ulicích rozehřát.

Voda má poměrně velkou tepelnou kapacitu, proto je energeticky náročné ji ohřát. Využívá se jako chladicí médium (odebere hodně tepla a moc se neohřeje) – viz např. při destilaci, k chlazení motorů, jaderných reaktorů aj.

Také pranostika „Únor bílý, pole sílí“ souvisí s tepelnou kapacitou. Sníh na poli působí jako izolant a brání vymrznutí půdy. Teplota pod sněhem je okolo 0 °C. Pokud by vrstva sněhu na poli neležela, v půdě by klesla teplota podle okolní třeba až na –20 °C. Mluvili bychom o tzv. holomrazech.

Sníh a led jako izolant využívají i Eskymáci. Za polární zimy klesá teplota venku až na – 60 °C. Na vnitřní straně iglú má led 0 °C. Vyšší teplotu led mít nemůže, protože by začal tát. Eskymáci vykládají stěny kožešinami. Když zapálí několik lampiček na tulení tuk, teplota uvnitř iglú je pak i přes 20 °C.

Teplé oblečení nošené v zimě také využíváme jako izolant. Ztrácíme méně tepla, „cítíme se zahříváni“.

U látek s vysokou hodnotou tepelné kapacity trvá déle, než se ohřejí, ale pak také pozvolna chladnou. Což lze pozorovat v přímořských oblastech, kde jsou v porovnání s vnitrozemním podnebím menší rozdíly mezi denní a noční teplotou nebo letními a zimními teplotami.

5.2.5.2

Kalorimetrie a kalorimetrická rovnice

Kalorimetrie je část termiky, která se zabývá měřením tepla. K měření se používá kalorimetr, což je v podstatě tepelně izolovaná nádoba. V laboratorním a průmyslovém prostředí se pro tepelně izolovanou nádobu používá název Dewarova nádoba neboli „dewarka“. Mohou mít kovový plášť a uvnitř super izolační fólií ve vakuovaném prostoru, nebo skleněnou nádobu s dvojitými postříbřenými stěnami a vakuovaným prostorem mezi nimi, takže odrážejí vnější i vnitřní tepelné vyzařování. Z domácnosti ji známe v podobě termosky.

Měření tepla se skládá ze dvou částí:

Stanovení tepelné kapacity kalorimetru K pomocí teplé a studené vody:

Příklad

Q_{d o d a n é} = Q_{p ř i j a t é}

Q = m \cdot c \cdot ∆ t

m_{2} \cdot c \cdot (t_{2} - t) = m_{1} \cdot c \cdot (t - t_{1}) + K \cdot (t - t_{1})

Zobrazit řešení

Skrýt řešení

Řešení

m₁... hmotnost studené vody na začátku měření (t ≅ 16 °C)

m₂ ... hmotnost teplé vody přidávané k soustavě (t ≅ 28 °C)

K ... tepelná kapacita kalorimetru

c ... specifická tepelná kapacita vody

t₁ ... naměřená teplota na začátku měření

t₂ ... naměřená teplota přidávané vody

t ... naměřená teplota po ustálení nebo zjištěná graficky z naměřených hodnot

Vlastní měření tepla ΔH (neutralizačního, rozpouštěcího, spalného, ...):

Příklad

∆ H = K \cdot ∆ t + m \cdot c \cdot ∆ t

Výsledek v J přepočteme na J ∙ g^-1 nebo J ∙ mol^-1.

Zobrazit řešení

Skrýt řešení

Řešení

Δt ... rozdíl teplot na začátku měření a po ustálení, popř. z grafu

m ... hmotnost reakční směsi

Obr. 29. Části kalorimetru [30]