Úvod do pravděpodobnosti

3.4

Vybraná rozdělení spojité náhodné veličiny

V této části se budeme věnovat některým pravděpodobnostním rozdělením spojité náhodné veličiny. K popisu těchto rozdělení budeme využívat hustotu pravděpodobnosti a distribuční funkci. Jednotlivá rozdělení zde budou popsána, budou uvedeny příklady jejich použití a také charakteristiky (střední hodnota a rozptyl) náhodné veličiny.

Jak už bylo napsáno dříve, v současné době se téměř veškeré statistické výpočty provádí za pomocí výpočetní techniky. V případě spojitých pravděpodobnostních rozdělení to platí dvojnásob, neboť se zde pracuje s integrály a derivacemi funkcí. V tomto výukovém materiálu bude pozornost věnována hlavně ukázce principu výpočtu a vše bude demonstrováno na zjednodušených příkladech, které je možné řešit pouze za pomoci kalkulačky. V závěru této části je opět uveden stručný návod, kde je popsána možnost využití MS Excelu pro řešení této problematiky.

ROVNOMĚRNÉ ROZDĚLENÍ

Rovnoměrné rozdělení řadíme mezi nejjednodušší pravděpodobnostní rozdělení spojité náhodné veličiny. Toto pravděpodobnostní rozdělení využijeme tam, kde má náhodná veličina X konstantní hustotu pravděpodobnosti na celém definičním oboru. Jinak řečeno, má stejnou možnost výskytu v celém intervalu

〈a; b〉

. Příkladem využití tohoto rozdělení v praxi může být čekání na odjezd dopravního prostředku (v pravidelném časovém intervalu) nebo chyby při zaokrouhlování.

Definice

Náhodná veličina X se přibližně řídí rovnoměrným rozdělením s parametry a a b:

X ~ R (a; b)

Hustotu pravděpodobnosti náhodné veličiny s rovnoměrným rozdělením je možné vyjádřit jako:

f (x) = \{\begin{matrix} \frac{1}{b - a}, a < x < b \\ 0, j i n a k \end{matrix}

Distribuční funkci je možné zapsat takto:

F (x) = \{\begin{matrix} 0, x \leq a \\ \frac{x - a}{b - a}, a < x < b \\ 1, x \geq b \end{matrix}

Poznámka

Nenechte se zmást zvláštním způsobem zápisu hustoty pravděpodobnosti a distribuční funkce, kde se vyskytuje veliká složená závorka (pouze její levá část). Jedná se o zápis, který zachycuje všechny části těchto funkcí. Např. u distribuční funkce rovnoměrného rozdělení první řádek říká, že pokud je x menší než dolní hranice a, pak je distribuční funkce nulová. Druhý řádek znamená, že pokud se x pohybuje mezi a a b, pak je možné distribuční funkci vypočítat podle tohoto výrazu

\frac{x - a}{b - a}

. Ve třetím řádku je řečeno, že pokud x nabude hodnoty stejné nebo větší než horní hranice b, pak se bude distribuční funkce rovnat jedné. Doporučuji podívat se na obr. 20, zde je vše názorně ukázáno.

Definice

Střední hodnota rovnoměrného rozdělení se vypočítá takto:

E (X) = \frac{a + b}{2}

Rozptyl rozdělení zapíšeme tímto způsobem:

D (X) = \frac{{(b - a)}^{2}}{12}

Obr. 19. Hustota pravděpodobnosti rovnoměrného rozdělení

Obr. 20. Distribuční funkce rovnoměrného rozdělení

Příklad

Pražské metro na trase C jezdí v době dopravní špičky v pravidelných tříminutových intervalech.

Jaká je pravděpodobnost, že pokud právě přijdeme v náhodně vybraný okamžik na stanici metra, přijede souprava do minuty?

Jaká je střední hodnota a rozptyl pro toto rozdělení?

Zobrazit řešení

Řešení

Dosadíme do vzorce pro výpočet distribuční funkce rovnoměrného rozdělení

F (x) = \frac{x - a}{b - a}

Ze zadání je jasné, že:

a = 0

b = 3

Náhodná veličina X se řídí rovnoměrným rozdělením v následujícím tvaru:

X ~ R (0; 3)

X \leq 1

F (1) = \frac{1 - 0}{3 - 0} \dot{=} 0, \bar{33}

Střední hodnota rovnoměrného rozdělení se vypočítá jako:

E (X) = \frac{a + b}{2} = \frac{0 + 3}{2} = 1,5

Průměrná doba do příjezdu soupravy pražského metra na trase C v době dopravní špičky je 1,5 minuty.

Rozptyl rozdělení zapíšeme tímto způsobem:

D (X) = \frac{{(b - a)}^{2}}{12} = \frac{{(3 - 0)}^{2}}{12} = \frac{9}{12} = 0,75

EXPONENCIÁLNÍ ROZDĚLENÍ

Exponenciální rozdělení se používá nejčastěji při výpočtu pravděpodobnosti doby životnosti výrobku, modelování času radioaktivního rozpadu a v systémech hromadné obsluhy. Náhodná veličina X označuje dobu, během které nastane sledovaný jev. Exponenciální rozdělení má dva parametry A a δ. „Parametr A představuje počáteční dobu, během které sledovaný jev nastat nemůže. Může to být například doba, během které trvá ověření platební karty při době obsluhy. Většinou však tato doba bývá nulová a hovoříme pak o jednoparametrickém exponenciálním rozdělení.“ [1]

Definice

Náhodná veličina X se přibližně řídí exponenciálním rozdělením s parametry A a δ:

X ~ E x p (A; δ)

Hustotu pravděpodobnosti náhodné veličiny s exponenciálním rozdělením je možné vyjádřit jako:

f (x) = \{\begin{matrix} \frac{1}{δ} e^{- \frac{(x - A)}{δ}}, x > A \\ 0, j i n a k \end{matrix}

Distribuční funkci můžeme zapsat takto:

F (x) = \{\begin{matrix} 0, x \leq A \\ 1 - e^{- \frac{(x - A)}{δ}}, x > A \end{matrix}

Definice

Střední hodnota exponenciálního rozdělení se vypočítá takto:

E (X) = A + δ

Rozptyl exponenciálního rozdělení zapíšeme následovně:

D (X) = δ^{2}

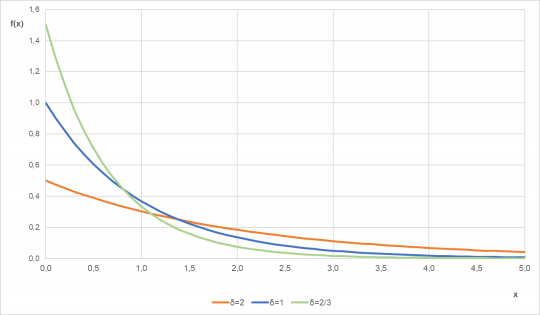
Obr. 21. Hustota pravděpodobnosti exponenciálního rozdělení pro různé parametry

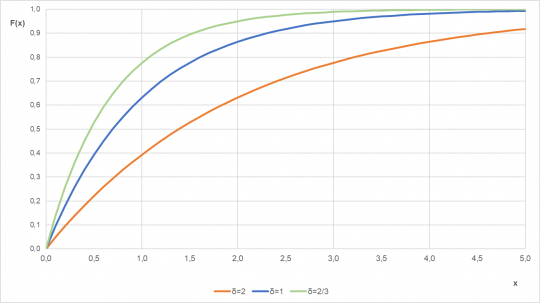
Obr. 22. Distribuční funkce exponenciálního rozdělení pro různé parametry

Příklad

Doba životnosti mikrovlnné trouby se řídí exponenciálním rozdělením se střední hodnotou 5 000 hodin.

Jaká je pravděpodobnost, že se mikrovlnná trouba porouchá během prvních 1 000 hodin?

Jaká je střední hodnota a rozptyl pro toto rozdělení?

Zobrazit řešení

Řešení

Dosadíme do vzorce pro výpočet distribuční funkce exponenciálního rozdělení

F (x) = 1 - e^{- \frac{(x - A)}{δ}}

Ze zadání je jasné, že:

A = 0

Parametr A je roven nule, protože mikrovlnná trouba se může porouchat okamžitě po prvním spuštění.

δ = 5 000

Náhodná veličina X se řídí exponenciálním rozdělením v následujícím tvaru:

X ~ E x p (0; 5 000)

X \leq 1 000

P (X \leq 1 000) = F (1 000) = 1 - e^{- \frac{(1000 - 0)}{5000}} \dot{=} 0,181

Pravděpodobnost, že se mikrovlnná trouba porouchá během prvních 1 000 hodin provozu, se rovná 0,181.

Střední hodnota exponenciálního rozdělení se vypočítá jako:

E (X) = A + δ = 0 + 5 000 = 5 000

Průměrná doba do poruchy mikrovlnné trouby je 5 000 hodin.

Rozptyl exponenciálního rozdělení vypočítáme jako druhou mocninu δ

D (X) = δ^{2} = {5 000}^{2} = 25 000 000

NORMÁLNÍ ROZDĚLENÍ

Normální rozdělení je nejdůležitějším pravděpodobnostním rozdělením. Využíváme ho jako pravděpodobnostní model pro chování mnoha náhodných jevů z oblasti přírodních věd, techniky i ekonomie. „Klasickým příkladem tohoto rozdělení je rozdělení náhodných chyb vzniklých při měření nějaké veličiny. Při opakovaném měření téže veličiny za stejných podmínek způsobují náhodné (nekontrolovatelné) vlivy odchylky od skutečné hodnoty měřené veličiny.“ [1]Řídí se jím náhodná veličina, jejíž kolísání je způsobeno součtem drobných, vzájemně nezávislých vlivů. Normální rozdělení má dva parametry μ a

σ^{2}

, které jsou zároveň střední hodnotou a rozptylem náhodné veličiny. Pomocí normálního rozdělení můžeme aproximovat (upravit) řadu jiných rozdělení, spojitých i nespojitých. „Předpoklad normality rozdělení je požadavek mnoha statistických metod a jeho porušení má více či méně negativní důsledky na výsledky a možnost aplikace jednotlivých metod.“ [1]

Definice

Náhodná veličina X se přibližně řídí normálním rozdělením s parametry μ a

σ^{2}

X ~ N (μ; σ^{2})

Hustotu pravděpodobnosti náhodné veličiny s normálním rozdělením (tzv. Gaussovu křivku) můžeme zapsat jako:

f (x) = \frac{1}{\sqrt{2 π σ^{2}}} e^{\frac{- {(x - μ)}^{2}}{2 σ^{2}}}

kde

- \infty < x < \infty,

- \infty < μ < \infty

σ^{2} > 0

Distribuční funkce má tento tvar:

F (x) = \frac{1}{σ \sqrt{2 π}} \int_{- \infty}^{x} e^{\frac{- {(t - μ)}^{2}}{2 σ^{2}}} d t

Poznámka

Abychom nemuseli počítat integrály a derivace funkcí, využijeme transformace náhodné veličiny X na normovanou náhodnou veličinu U, která je tabelována. Postup jejího výpočtu je uveden dále.

Definice

Střední hodnota normálního rozdělení se vypočítá takto:

E (X) = μ

Rozptyl normálního rozdělení zapíšeme jako:

D (X) = σ^{2}

Obr. 23. Hustota pravděpodobnosti normálního rozdělení pro různé parametry

Z obrázku 23 je jasně zřetelné, proč se o normálním rozdělení říká, že je symetrické kolem střední hodnoty. U normálního rozdělení vždy platí, že střední hodnota se rovná také modu (nejčastěji zastoupené hodnotě v souboru) a mediánu (polovina uspořádaného souboru).

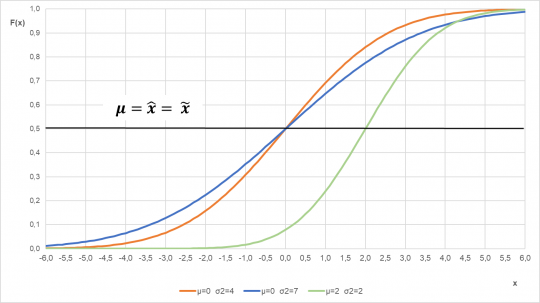
Obr. 24. Distribuční funkce normálního rozdělení pro různé parametry

Pro zjednodušení se většinou používá normované normální rozdělení, které je speciálním případem normálního rozdělení. Hodnoty tohoto rozdělení jsou tabelovány (zapsány v tabulkách), což značně usnadňuje výpočty.

Definice

Náhodná veličina U se řídí normovaným normálním rozdělením s parametry

μ = 0

σ^{2} = 1

, tzn. normálním rozdělením se střední hodnotou 0 a rozptylem 1:

U ~ N (0; 1)

Transformaci náhodné veličiny X na normovanou normální veličinu U provádíme pomocí tohoto výrazu:

U = \frac{X - μ}{σ}

X ~ N (μ; σ^{2})

Hustotu pravděpodobnosti náhodné veličiny s normovaným normálním rozdělením zapíšeme jako:

f (u) = \frac{1}{\sqrt{2 π}} e^{\frac{- {(u)}^{2}}{2}}

kde

- \infty < u < \infty .

Distribuční funkce má tento tvar:

Φ (u) = \frac{1}{\sqrt{2 π}} \int_{- \infty}^{u} e^{\frac{- {(t)}^{2}}{2}} d t

Poznámka

Ve chvíli, kdy zapisujeme distribuční funkci normované normální veličiny U, změníme i označení samotné distribuční funkce na

Φ

. Pokud tedy hovoříme o distribuční funkci normální veličiny, píšeme F(x), když o distribuční funkci normované normální veličiny, pak

Φ (u)

Definice

Střední hodnota normovaného normálního rozdělení se vypočítá takto:

E (U) = 0

Rozptyl normovaného normálního rozdělení zapíšeme jako:

D (U) = 1

Kvantil normovaného normálního rozdělení vypočítáme pomocí následujícího výrazu:

x_{p} = µ + σ u_{p}

Definice

Distribuční funkce normované normální veličiny je symetrická kolem nuly a platí pro ni:

Φ (- u) = 1 - Φ (u)

Pro kvantily normovaného normálního rozdělení platí tento vztah:

u_{p} = - u_{1 - p}

Jestliže potřebujeme nalézt pravděpodobnost, že náhodná veličina X nabývá hodnoty z intervalu

〈x_{1}; x_{2}〉

, poslouží nám tento zápis:

P (x_{1} \leq X \leq x_{2}) = P (\frac{x_{1} - μ}{σ} < \frac{X - μ}{σ} < \frac{x_{2} - μ}{σ}) = P (u_{1} \leq U \leq u_{2})

Díky vlastnostem distribuční funkce můžeme tento zápis ještě upravit do následujícího tvaru:

P (u_{1} \leq U \leq u_{2}) = Φ (u_{2}) - Φ (u_{1})

Video 4. Příklad na normované normální rozdělení

Příklad

Automat plní moukou balíky o váze 5 kg. Náhodná veličina X představuje odchylku v gramech (chybu plnění) od požadované hodnoty 5 kg. Tato chyba má normální rozdělení s parametry μ = 0 a σ²= 64.

Určete:

pravděpodobnost, že váha balíku bude větší než 5 016 g,

pravděpodobnost, že se váha balíku bude pohybovat v intervalu $〈4 995; 5 005〉$ ,

takovou hodnotu x, kterou odchylka od průměrné váhy balíku nepřekročí s pravděpodobností 0,99.

takovou hodnotu x, pro kterou se odchylka od průměrné váhy balíku s pravděpodobností 0,9 bude pohybovat v intervalu $〈- x; x〉$ .

Jaká je střední hodnota a rozptyl pro toto rozdělení?

Zobrazit řešení

Řešení

Ve všech případech budeme dosazovat do vzorců pro normovanou normální veličinu.

Ze zadání je jasné, že

μ = 0

σ^{2} = 64

Náhodná veličina X se řídí normálním rozdělením v následujícím tvaru:

X ~ N (0; 64)

pravděpodobnost, že váha balíku bude větší než 5 016 g

X > 16

Zde je nutné řešit vše přes doplňkový jev. To, že váha balíku bude větší minimálně o 16 gramů neumíme matematicky vyřešit jinak než jako „1 - distribuční funkce v hodnotě 16“.

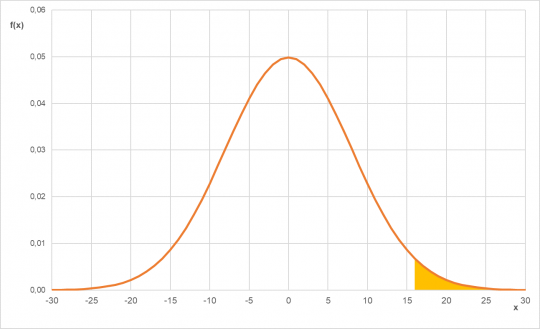
Obr. 25. Pravděpodobnost P(X > 16) pro normální rozdělení N(0;64)

P (X > 16) = 1 - P (X \leq 16) = 1 - P (U \leq u) = 1 - P (U \leq \frac{X - μ}{σ}) = 1 - P (U \leq \frac{16 - 0}{8}) = 1 - P (U \leq 2) = 1 - Φ (2) = 1 - 0,97725 = 0,02275

Pravděpodobnost, že automat balík mouky přesype o více než 16 gramů, se rovná přibližně 0,023.

pravděpodobnost, že se váha balíku bude pohybovat v intervalu $〈4995; 5005〉$

U tohoto zadání se nenechte zmást tím, že je uvedena váha balíku. Nás zajímá jen odchylka od střední hodnoty 5 000 gramů, což je

\pm 5

gramů.

- 5 \leq X \leq 5

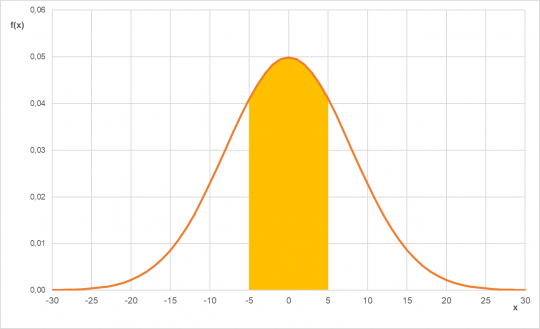
26. Pravděpodobnost pro normální rozdělení N(0;64)

Obr. 26. Pravděpodobnost

P (- 5 \leq X \leq 5)

pro normální rozdělení N(0;64)

P (- 5 \leq X \leq 5) = P (u_{1} \leq U \leq u_{2}) = P (\frac{- 5 - 0}{8} U \leq \frac{5 - 0}{8}) = P (- 0,625 \leq U \leq 0,625) = Φ (0,625) - Φ (- 0,625) = Φ (0,625) - (1 - Φ (0,625)) = 2 \times Φ (0,625) - 1 = 2 \times 0,734 - 1 = 0,468

Pravděpodobnost, že se balík mouky bude odchylovat od průměru o

\pm 5

gramů, je rovna 0,468.

takovou hodnotu x, kterou odchylka od průměrné váhy balíku nepřekročí s pravděpodobností 0,99

V tomto zadání se již neptáme na to, s jakou pravděpodobností něco (ne)nastane. Pravděpodobnost je dána a nás zajímá, pro jaké x toto platí. Tento typ úloh se řeší pomocí kvantilů.

P (X \leq x) = 0,99

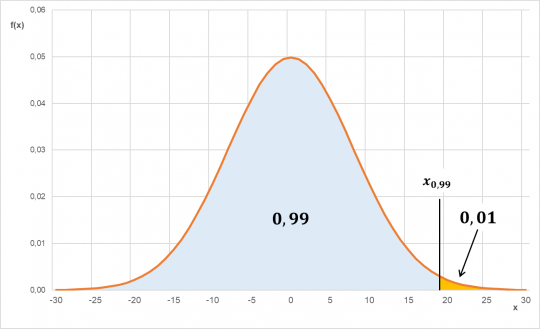
Obr. 27. Kvantil x_0,99 pro normální rozdělení N(0;64)

x_{p} = μ + σ {\times u}_{p}

Budeme hledat 99% kvantil.

x_{0,99} = μ + σ {\times u}_{0,99} = 0 + 8 \times 2,326 \dot{=} 18,61

S pravděpodobností 0,99 odchylka od průměrné váhy balíku nepřekročí 18,61 gramů.

takovou hodnotu x, pro kterou se odchylka od průměrné váhy balíku s pravděpodobností 0,9 bude pohybovat v intervalu $〈- x; x〉$

Toto zadání budeme také řešit pomocí kvantilů, ale pozor, nehledáme jedno x, ale dvě, tudíž kvantily budou také dva.

P (x_{1} \leq X \leq x_{2}) = 0,9

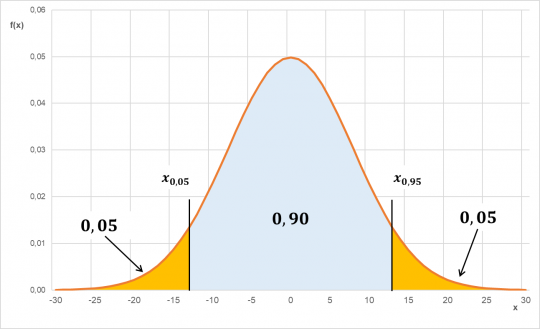
Obr. 28. Kvantil x_0,05 a x_0,95 pro normální rozdělení N(0;64)

x_{p} = μ + σ {\times u}_{p}

Budeme hledat 5% a 95% kvantil.

x_{0,95} = μ + σ {\times u}_{0,95} = 0 + 8 \times 1,645 \dot{=} 13,16

x_{0,05} = μ + σ {\times u}_{0,05} = 0 + 8 \times (- 1,645) \dot{=} - 13,16

S pravděpodobností 0,9 se odchylka od průměrné váhy balíku bude pohybovat v intervalu

〈- 13,16; 13,16〉

gramů.

Jaká je střední hodnota a rozptyl pro toto rozdělení?

Střední hodnota normálního rozdělení se rovná

E (X) = μ = 0

Průměrná odchylka od balíku vážícího 5 kg je rovna nule.

Rozptyl normálního rozdělení vyjádříme takto

D (X) = σ^{2} = 64

LOGARITMICKO-NORMÁLNÍ ROZDĚLENÍ

Definice

Logaritmicko-normální rozdělení, někdy se také můžeme setkat s kratším označením lognormální rozdělení, je rozdělení náhodné veličiny, která má tento tvar:

X = e^{Y}

kde

Y ~ N (μ; σ^{2})

Náhodná veličina X se přibližně řídí logaritmicko-normálním rozdělením s parametry μ a

σ^{2}

X ~ L N (μ; σ^{2})

Hustotu pravděpodobnosti náhodné veličiny s logaritmicko-normálním rozdělením můžeme zapsat jako:

f (x) = \{\begin{matrix} \frac{1}{x σ \sqrt{2 π}} e^{\frac{- {(l n x - μ)}^{2}}{2 σ^{2}}}, x > 0 \\ 0, j i n a k \end{matrix}

Distribuční funkci logaritmicko-normálního rozdělení můžeme určit pomocí distribuční funkce normovaného normálního rozdělení:

F (x) = \{\begin{matrix} \frac{l n x - μ}{σ}, x > 0 \\ 0, j i n a k \end{matrix}

Tímto rozdělením se řídí např. příjmová rozdělení a je tzv. kladně sešikmené, viz obrázek 29.

Poznámka

Na rozdíl od normálního rozdělení se v případě logaritmicko-normálního parametry

μ

σ^{2}

nerovnají střední hodnotě a rozptylu pro toto rozdělení.

Definice

Střední hodnota logaritmicko-normálního rozdělení se vypočítá takto:

E (X) = e^{μ + \frac{σ^{2}}{2}}

Rozptyl logaritmicko-normálního rozdělení zapíšeme jako:

D (X) = e^{2 μ + σ^{2}} (e^{σ^{2}} - 1)

Pro p% kvantily logaritmicko-normálního rozdělení platí:

x_{p} = e^{(μ + σ u_{p})}

kde

u_{p}

značí p-procentní kvantil normovaného normálního rozdělení.

Obr. 29. Hustota pravděpodobnosti logaritmicko-normálního rozdělení pro různé parametry

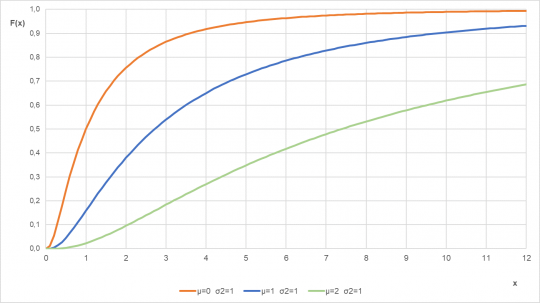
Obr. 30. Distribuční funkce logaritmicko-normálního rozdělení pro různé parametry

Příklad

Vypočítejte hodnotu distribuční funkce logaritmicko-normálního rozdělení

L N (1; 9)

v bodě

x = 3

a 90% kvantil.

Zobrazit řešení

Řešení

Distribuční funkci logaritmicko-normálního rozdělení určujeme pomocí normované normální veličiny

U = \frac{l n x - μ}{σ}

F (5) = F (\frac{l n x - μ}{σ}) = F (\frac{l n 5 - 1}{3}) \dot{=} F (\frac{1,099 - 1}{3}) \dot{=} F (0,033) \dot{=} 0,513

90% kvantil vypočítáme podle tohoto výrazu

x_{p} = e^{(μ + σ u_{p})}

x_{0,90} = e^{(μ + σ {\times u}_{0,90})} \dot{=} e^{(1 + 3 \times 1,282)} \dot{=} 127,1

Následující rozdělení budou popsána jen v krátkosti, protože výpočet jejich hustoty pravděpodobnosti i distribuční funkce není jednoduchý. Avšak jedná se o velmi důležitá rozdělení, která jsou hojně využívána v oblasti matematické statistiky (teorie odhadů, testování hypotéz).

CHÍ-KVADRÁT ROZDĚLENÍ

„Chí-kvadrát rozdělení má rozsáhlé použití v teorii odhadu a testování hypotéz, zejména při ověřování předpokladu, zda empirické rozdělení četností má či nemá pravděpodobnostní rozdělení určitého druhu, při ověřování nezávislosti kvalitativních znaků a jinde.“ [1]

Definice

Jsou-li U₁, U₂, …, U_v nezávislé náhodné veličiny, z nichž každá má normované normální rozdělení N(0;1), pak součet čtverců těchto náhodných veličin je veličinou

χ^{2}

χ^{2} = \sum_{i = 1}^{ν} U_{i}^{2}

kde

ν

je počet stupňů volnosti, který označuje počet nezávislých sčítanců.

Výpočet hustoty pravděpodobnosti pro chí-kvadrát rozdělení je velmi komplikovaný, takže zde nebude uváděn.

Definice

Střední hodnota chí-kvadrát rozdělení se vypočítá takto:

E (χ^{2}) = ν

Rozptyl chí-kvadrát rozdělení zapíšeme jako:

D (χ^{2}) = 2 ν

Pro různé kombinace υ a p jsou hodnoty kvantilů rozdělení

χ^{2} (ν)

tabelovány. Pro daný počet stupňů volnosti musí být splněn vztah

(χ^{2} < χ_{p}^{2}) = p

. S rostoucím počtem stupňů volnosti se chí-kvadrát rozdělení blíží normálnímu rozdělení.

Definice

Pro

ν > 30

je možné kvantily chí-kvadrát rozdělení stanovit pomocí kvantilů normovaného normálního rozdělení:

χ_{p}^{2} [ν] \approx \frac{1}{2} {(u_{p} + \sqrt{2 ν - 1})}^{2}

kde

u_{p}

značí p-procentní kvantil normovaného normálního rozdělení.

Obr. 31. Hustota pravděpodobnosti chí-kvadrát rozdělení pro různé parametry

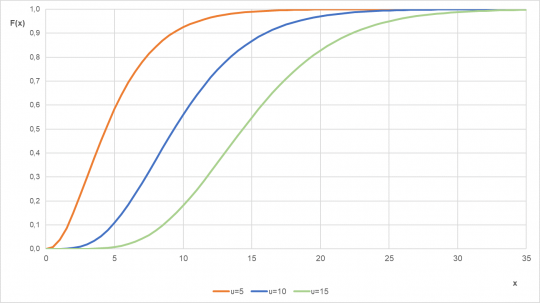
Obr. 32. Distribuční funkce chí-kvadrát rozdělení pro různé parametry

ROZDĚLENÍ T (STUDENTOVO)

Rozdělení t je kombinací nám již známého normovaného normálního rozdělení a chí-kvadrát rozdělení. Za jeho vznikem stojí Angličan William Sealy Gosset (1876–1937), který publikoval pod pseudonymem Student. „[William Sealy Gosset] nebyl povoláním statistikem, jak by se opět dalo očekávat. Byl povoláním chemik a začátkem našeho století pracoval v anglickém pivovaru Guinness. A toto rozdělení nevymyslel proto, že by se nudil, ale proto, že potřeboval vyvozovat na základě velmi malých vzorků použitelné závěry. A k těmto účelům se toto rozdělení používá dodnes.“ [5]Často se s tímto rozdělením můžeme setkat v matematické statistice, konkrétně při odhadech a testování hypotéz. „Užívá se k testování hypotéz o střední hodnotě náhodného výběru, pokud je rozptyl neznámý… Užívá se k testování hypotéz o shodě středních hodnot dvou náhodných výběrů… t rozdělení je vhodným prostředkem pro analýzu výsledků regresní analýzy.“ [5]

Definice

Uvažujme dvě nezávislé náhodné veličiny U(0;1) a

χ^{2} (ν)

Veličina t má Studentovo rozdělení:

t = \frac{U}{\sqrt{\frac{χ^{2}}{ν}}}

kde

ν

je počet stupňů volnosti.

Pro

ν \to \infty

se t rozdělení blíží normovanému normálnímu. V praxi, pokud platí, že

ν > 30

, pak t rozdělení je již považováno za normální.

Obr. 33. Hustota pravděpodobnosti t rozdělení pro různé parametry

Obr. 34. Distribuční funkce t rozdělení pro různé parametry

Pro různé kombinace υ a p jsou hodnoty kvantilů rozdělení

t (ν)

tabelovány.

ROZDĚLENÍ F (FISHEROVO-SNEDECOROVO)

Rozdělení F je odvozeno od podílu dvou nezávislých náhodných veličin, které se řídí chí-kvadrát rozdělením dělených stupni volnosti. Rozdělení bývá také označováno Fisherovo-Snedecorovo rozdělení, podle Ronalda Fishera (1890–1962) a George W. Snedecora (1881–1974). I toto rozdělení má své uplatnění v oblasti matematické statistiky. „Toto rozdělení má opět široké uplatnění, především při hodnocení výsledků statistických analýz. Používá se především: K testu o shodnosti rozptylů dvou náhodných výběrů. K testům o shodě středních hodnot pro více náhodných výběrů. K testům v regresní analýze.“ [5]

Definice

Uvažujme dvě nezávislé náhodné veličiny

χ_{1}^{2} (ν_{1})

χ_{2}^{2} (ν_{2})

Náhodná veličina F má Fisherovo-Snedecorovo rozdělení:

F = \frac{\frac{χ_{1}^{2}}{ν_{1}}}{\frac{χ_{2}^{2}}{ν_{2}}}

kde

ν_{1}

ν_{2}

je počet stupňů volnosti.

Toto rozdělení má dva parametry, kterými jsou stupně volnosti

ν_{1}

ν_{2}

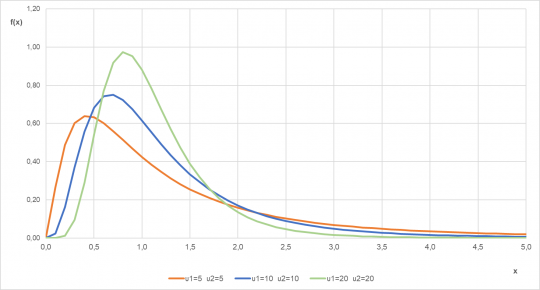
Obr. 35. Hustota pravděpodobnosti F rozdělení pro různé parametry

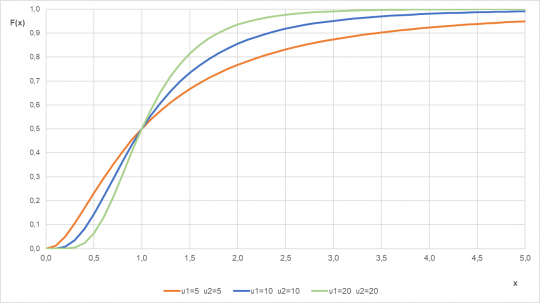
Obr. 36. Distribuční funkce F rozdělení pro různé parametry

Pro různé kombinace

ν_{1}

ν_{2}

jsou hodnoty kvantilů rozdělení

F (ν_{1}; ν_{2})

tabelovány.

Souhrn

Rovnoměrné rozdělení řadíme mezi nejjednodušší pravděpodobnostní rozdělení spojité náhodné veličiny. Příkladem využití tohoto rozdělení v praxi může být čekání na odjezd dopravního prostředku (v pravidelném časovém intervalu) nebo chyby při zaokrouhlování. Exponenciální rozdělení se používá nejčastěji při výpočtu pravděpodobnosti doby životnosti výrobku, modelování času radioaktivního rozpadu a v systémech hromadné obsluhy. Náhodná veličina X označuje dobu, během které nastane sledovaný jev. Normální rozdělení je nejdůležitějším pravděpodobnostním rozdělením. Využíváme ho jako pravděpodobnostní model pro chování mnoha náhodných jevů z oblasti přírodních věd, techniky i ekonomie. Příkladem je rozdělení náhodných chyb vzniklých při měření nějaké veličiny. Pomocí normálního rozdělení můžeme aproximovat (upravit) řadu jiných rozdělení, spojitých i nespojitých. Logaritmicko-normální rozdělení je tzv. kladně sešikmené a řídí se jím např. příjmová rozdělení. Chí-kvadrát rozdělení má rozsáhlé použití v teorii odhadu a testování hypotéz, zejména při ověřování předpokladu, zda empirické rozdělení četností má či nemá pravděpodobnostní rozdělení určitého druhu, při ověřování nezávislosti kvalitativních znaků a jinde. T rozdělení je vhodným prostředkem pro analýzu výsledků regresní analýzy. Rozdělení F je odvozeno od podílu dvou nezávislých náhodných veličin, které se řídí chí-kvadrát rozdělením, dělených stupni volnosti a uplatňuje se především při hodnocení výsledků statistických analýz.

Poznámka

MS EXCEL

Pro výpočet pravděpodobnostních rozdělení můžeme využít jednotlivé statistické funkce.

Před název funkce vždy napíšeme „=“, pak následuje název funkce bez mezer a závorky, do kterých se umístí jednotlivé parametry. Bohužel popis parametrů, který se v Excelu uvádí, není vždy úplně intuitivní. Proto jsou zde uvedeny i dva sloupce, kde jsou zapsány názvy parametrů z Excelu a jim odpovídají pořadí parametrů, které již známe z oblasti pravděpodobnosti.

Poslední parametr u funkcí, které počítají v MS Excelu pravděpodobnostní rozdělení, rozhoduje o tom, zda jde o výpočet pravděpodobnostní funkce (zapíše se číslo 0) nebo distribuční funkce (zapíše se číslo 1) v daném bodě.

Výpočet, který chceme provést	Parametry funkce	Funkce v MS Excelu	Označení parametrů funkce v MS Excelu
Exponenciální rozdělení	(x; $A; δ$ )	EXPON.DIST	(x; lambda; kumulativní)
Normální rozdělení	(x; μ; σ²)	NORM.DIST	(x; střed_hodn; sm_odch; kumulativní)
Logaritmicko-normální rozdělení	(x; μ; σ²)	LOGNORM.DIST	(x; střední; sm_odchylka; kumulativní)
Chí-kvadrát rozdělení	( $x; ν$ )	CHISQ.DIST	(x; volnost; kumulativní)
Rozdělení t	(x; $ν;$ t)	T.DIST T.DIST.2T T.DIST.RT	(x; volnost; kumulativní) (x; volnost) (x; volnost)
Rozděleni F	$(x; ν_{1}$ ; $ν_{2}$ )	F.DIST	(x; volnost; volnost; kumulativní)

V případě, že potřebujete vypočítat kvantily těchto rozdělení, zpravidla je začátek funkce v MS Excel stejný, ale místo „DIST“ je použita koncovka „INV“.

Výpočet, který chceme provést	Parametry funkce	Funkce v MS Excelu	Označení parametrů funkce v MS Excelu
Kvantily normálního rozdělení	(p; μ; σ²)	NORM.INV	(pravděpodobnost; střední; sm_odch)
Kvantily logaritmicko-normálního rozdělení	(p; μ; σ²)	LOGNORM.INV	(pravděpodobnost; stř_hodn; sm_odch)
Kvantily chí-kvadrát rozdělení	( $p; ν$ )	CHISQ.INV	(pravděpodobnost; volnost)
Kvantily rozdělení t	( $p; ν;$ t)	T.INV T.INV.2T	(pravděpodobnost; volnost) (pravděpodobnost; volnost)
Kvantily rozděleni F	$(p; ν_{1}$ ; $ν_{2}$ )	F.INV	(pravděpodobnost; volnost; volnost)