Úvod do pravděpodobnosti

3.1

Zákon rozdělení náhodné veličiny

Náhodnou veličinu můžeme pokládat za danou, jestliže známe všechny hodnoty, kterých může nabývat, resp. intervaly těchto hodnot, a pravděpodobnosti výskytu každé z hodnot, resp. pravděpodobnosti výskytu v určitém intervalu reálných čísel.

Definice

„Zákon rozdělení náhodné veličiny je pravidlo, které každé hodnotě nebo množině hodnot z určitého intervalu přiřadí pravděpodobnost, že náhodná veličina nabude právě této hodnoty nebo množiny hodnot z tohoto intervalu.“ [1]

Zákon rozdělení náhodné veličiny je možné vyjádřit různými způsoby v závislosti na typu náhodné veličiny. Pro nespojitou náhodnou veličinu rozlišujeme pravděpodobnostní funkci a distribuční funkci. Pro spojitou náhodnou veličinu rozlišujeme distribuční funkci a hustotu pravděpodobnosti.

PRAVDĚPODOBNOSTNÍ FUNKCE

„Pravděpodobností funkce je nejjednodušší forma popisu (forma vyjádření zákonu rozdělení) nespojité náhodné veličiny.“ [1]

Definice

Pravděpodobnostní funkce každému x přiřazuje pravděpodobnost, že náhodná veličina X nabude hodnoty právě x.

Budeme ji značit P(x) a je možné ji zapsat tímto vztahem

P (x) = P (X = x)

Díky pravděpodobnostní funkci jsme schopni určit pravděpodobnost výskytu konkrétní hodnoty u nespojité náhodné veličiny.

Pro pravděpodobnostní funkci platí tyto vlastnosti:

Pravděpodobnostní funkce nabývá hodnot od nuly do jedné, což plyne z axiomu o pravděpodobnosti náhodného jevu:

0 \leq P (x) \leq 1

Protože je jisté, že náhodná veličina nabude některé z hodnot x, součet všech hodnot pravděpodobnostní funkce je jedna:

\sum_{x} P (x) = 1

Poznámka

\sum_{x} P (x) = 1

– Tento způsob zápisu sumace nám říká, že se jedná o součet „přes všechny hodnoty x“. Není nutné, aby zde byla uvedena horní i dolní mez.

Můžeme stanovit i pravděpodobnost, že náhodná veličina leží v intervalu $〈x_{1}; x_{2}〉$ , vypočítáme jako součet hodnot pravděpodobnostních funkcí v bodech od x₁ do x₂ včetně:

P (x_{1} \leq X \leq x_{2}) = \sum_{x_{1}}^{x_{2}} P (x)

Pravděpodobnostní funkci můžeme vyjádřit různými způsoby, na ilustrativním příkladu si ukážeme, jak by to vypadalo.

Tento příklad se inspiroval zadáním příkladu 2.7 na straně 61 v knize [1].. Ve středně velké firmě se chystají provést sociologický průzkum mezi zaměstnanci. Předtím, než bude provedeno samotné šetření, rozhodlo se vedení firmy k provedení pilotního šetření na malém vzorku zaměstnanců, aby zjistilo, zda je pro ně dotazník srozumitelný, otázky jsou jednoznačné atp. Velikost pilotního vzorku je pět osob. Z údajů o celé firmě víme, že zde pracuje 40 % žen a 60 % mužů. Naším úkolem je určit pravděpodobnosti, že v pilotním vzorku bude 0, 1, 2, 3, 4 nebo 5 žen.

Náhodná veličina X představuje počet žen ve vzorku a konkrétní realizace výsledků mohou nabývat hodnot

x = 0, x = 1, x = 2, x = 3, x = 4 a x = 5

. Předpokládáme, že počty žen ve vzorku jsou nezávislými jevy, potom pravděpodobnost, že v pilotním vzorku nebude žádná žena (bude tam 5 mužů), je dána tímto vztahem:

P (x = 0) = P (0) = 0,6 \times 0,6 \times 0,6 \times 0,6 \times 0,6 \dot{=} 0,0778

Pravděpodobnost vybrání jedné ženy do vzorku může být zapsána takto:

P (x = 1) = P (1) = 0,4 \times 0,6 \times 0,6 \times 0,6 \times 0,6 \dot{=} 0,0518

Ovšem jak už víme, zde může nastat více variant, jak může být vybrána jedna žena a čtyři muži. Může nastat jiné uspořádání, kdy žena bude na 2., 3., 4. či 5. pozici ve výběru

P (x = 1) = P (1) = 0,6 \times 0,4 \times 0,6 \times 0,6 \times 0,6 \dot{=} 0,0518

P (x = 1) = P (1) = 0,6 \times 0,6 \times 0,4 \times 0,6 \times 0,6 \dot{=} 0,0518

P (x = 1) = P (1) = 0,6 \times 0,6 \times 0,6 \times 0,4 \times 0,6 \dot{=} 0,0518

P (x = 1) = P (1) = 0,6 \times 0,6 \times 0,6 \times 0,6 \times 0,4 \dot{=} 0,0518

Díky pravidlům kombinatoriky, je možné toto zjednodušeně zapsat v následujícím tvaru:

P (1) = (\binom{5}{1}) \times {0,4}^{1} \times {0,6}^{4} = 0,2592

Takto můžeme pokračovat pro všechny varianty výsledků:

P (2) = (\binom{5}{2}) \times {0,4}^{2} \times {0,6}^{3} = 0,3456

P (3) = (\binom{5}{3}) \times {0,4}^{3} \times {0,6}^{2} = 0,2304

P (4) = (\binom{5}{4}) \times {0,4}^{4} \times {0,6}^{1} = 0,0768

P (5) = (\binom{5}{5}) \times {0,4}^{5} \times {0,6}^{0} \dot{=} 0,0102

Takže prvním způsobem, jak vyjádřit pravděpodobnostní funkci je pomocí matematického výrazu:

P (x) = (\binom{n}{x}) π^{x} {(1 - π)}^{n - x}

Dalším způsobem vyjádření může být tabulka rozdělení pravděpodobnosti (zvaná též řada rozdělení).

x	0	1	2	3	4	5	∑
P(x)	0,0778	0,2592	0,3456	0,2304	0,0768	0,0102	1

Poznámka

Součet všech možných výsledků, kterých pravděpodobnostní funkce nabývá, musí být vždy roven jedné.

Další možností je graf, v našem případě je vhodné použít buď bodový graf, nebo sloupcový graf.

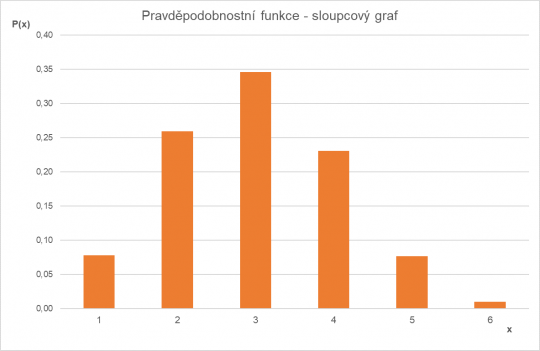
Obr. 11. Bodový graf pravděpodobnostní funkce

Poznámka

V případě nespojité funkce by jednotlivé výsledky vynesené v grafu neměly být spojeny čárou, protože pravděpodobnostní funkce těchto výsledků nenabývá. Může nabýt pouze celých čísel.

DISTRIBUČNÍ FUNKCE

„Distribuční funkce je forma popisu (forma vyjádření zákonu rozdělení) nespojité i spojité náhodné veličiny.“ [1]

Definice

Distribuční funkce je definována jako pravděpodobnost, že náhodná veličina X nabude hodnoty nejvýše x.

Budeme ji značit F(x) a je možné ji zapsat tímto vztahem:

F (x) = P (X \leq x)

Poznámka

Ze známé distribuční funkce můžeme odvodit pravděpodobnostní funkci a naopak.

Díky distribuční funkci jsme schopni určit pravděpodobnost výskytu všech hodnot, které se rovnají nebo jsou menší než zvolená hodnota.

Pro distribuční funkci platí tyto vlastnosti:

Distribuční funkce nabývá hodnot od nuly do jedné:

0 \leq F (x) \leq 1

Distribuční funkce je funkce neklesající, tj. pro každou dvojici čísel $x_{1} < x_{2}$ platí:

F (x_{1}) \leq F (x_{2})

F (x_{2}) - F (x_{1}) = P (x_{1} < X < x_{2})

Distribuční funkce je spojitá zprava.

Pro spojité náhodné veličiny platí:

F (x) = P (X < x) = P (X \leq x)

Pravděpodobnost, že náhodná veličina X nabude hodnoty z intervalu $(x_{1}; x_{2}⟩$ , je rovna rozdílu distribuční funkce v horní mezi a dolní mezi:

P (x_{1} < X \leq x_{2}) = F (x_{2}) - F (x_{1})

Obecně platí $F (- \infty) = 0, F (\infty) = 1$ .

Způsob výpočtu distribuční funkce se odvíjí od typu náhodné veličiny.

Pro nespojitou náhodnou veličinu se distribuční funkce vypočítá jako:

F (x) = P (X \leq x_{0}) = \sum_{x \leq x_{0}} P (x)

Pro spojitou náhodnou veličinu se distribuční funkce vypočítá jako:

F (x) = P (X \leq x_{0}) = \int_{- \propto}^{x_{0}} f (x) d x

kde f(x) je hustota pravděpodobnosti náhodné veličiny X, jak bude vysvětleno dále.

Opět si zde ukážeme možné vyjádření distribuční funkce pomocí matematického zápisu a použijeme data z ilustrativního příkladu, kde bylo prováděno pilotní šetření na vzorku pěti zaměstnanců. Využijeme data o pravděpodobnostech výskytu jednotlivých variant výsledků a budeme je nasčítávat (kumulovat) pro jednotlivé distribuční funkce.

x	0	1	2	3	4	5	∑
P(x)	0,0778	0,2592	0,3456	0,2304	0,0768	0,0102	1

F(x) = 0 pro x < 0, = 0,0778 pro 0 ≤ x <1, = 0,3370 pro 1 ≤ x <2, = 0,6826 pro 2 ≤ x <3, = 0,9130 pro 3 ≤ x <4, = 0,9898 pro 4 ≤ x <5, = 1 pro x ≥ 5.

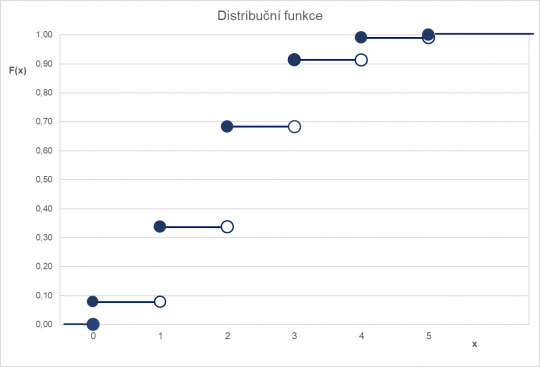
Obr. 12. Graf distribuční funkce nespojité náhodné veličiny

Z grafu distribuční funkce nespojité náhodné veličiny je jasně patrné, proč se o ní říká, že se jedná o funkci schodovitou, zprava spojitou a také neklesající.

HUSTOTA PRAVDĚPODOBNOSTI

„Hustota pravděpodobnosti je forma popisu spojité náhodné veličiny a je definována jako derivace distribuční funkce.“ [1]

Budeme ji značit f(x) a je možné ji zapsat tímto vztahem:

f (x) = F' (x)

Díky hustotě pravděpodobnosti jsme schopni určit pravděpodobnost, že náhodná veličina padne do velmi malého intervalu, který označíme

(x; x + ∆ x)

. Geometricky je vše znázorněno na obr. 13. „Pravděpodobnost padnutí hodnoty náhodné veličiny X mezi x a

x + ∆ x

je pro malé

∆ x

přibližně rovna ploše pravoúhelníku se základnou

∆ x

a výškou f(x).“ [1]

Obr. 13. Hustota pravděpodobnosti a rozdíl mezi přesnou pravděpodobností a součinem

∆ x \cdot f (x)

Pro hustotu pravděpodobnosti platí tyto vlastnosti:

Hustota pravděpodobnosti nabývá nezáporných hodnot:

f (x) \geq 0

Integrál hustoty pravděpodobnosti přes všechny hodnoty, kterých může náhodná veličina nabýt (celková plocha pod funkcí f(x)), je jedna:

\int_{- \infty}^{\infty} f (x) d x = 1

Pravděpodobnost, že náhodná veličina X nabude hodnoty z intervalu <x₁;x₂>, je rovna integrálu hustoty pravděpodobnosti v mezích <x₁;x₂>, což je rovno rozdílu distribuční funkce v horní mezi a dolní mezi:

P (x_{1} \leq X \leq x_{2}) = \int_{x_{1}}^{x_{2}} f (x) d x = F (x_{2}) - F (x_{1})

Poznámka

Rozdělení spojité náhodné veličiny lze popsat pravděpodobnostní funkcí v určitém bodě, z principu výpočtu derivace by ale tato hodnota vyšla limitně nulová!

Souhrn

Zákon rozdělení náhodné veličiny je pravidlo, které každé hodnotě nebo množině hodnot z určitého intervalu přiřadí pravděpodobnost, že náhodná veličina nabude právě této hodnoty nebo množiny hodnot z tohoto intervalu. Pro nespojitou náhodnou veličinu rozlišujeme pravděpodobnostní funkci a distribuční funkci. Pro spojitou náhodnou veličinu rozlišujeme distribuční funkci a hustotu pravděpodobnosti.