Graf řekne více než tisíc slov. Pomocí grafického zobrazení údajů je mnohdy možné předat čtenáři informaci srozumitelněji než slovním popisem. Pomocí jednoduchého a přehledného zobrazení statistických údajů můžeme rychle získat představu o charakteristických vlastnostech zkoumaných jevů. Grafy rozdělujeme podle způsobu jejich konstrukce na několik typů. Mezi nejčastěji používané typy grafů ve statistice patří histogram rozdělení četností a polygon rozdělení četností, sloupcový graf, výsečový graf a krabičkový graf. K jednotlivým grafům, a hlavně ke vhodnosti jejich použití pro konkrétní typy dat jsou uvedeny podrobnější informace níže.
SLOUPCOVÝ GRAF
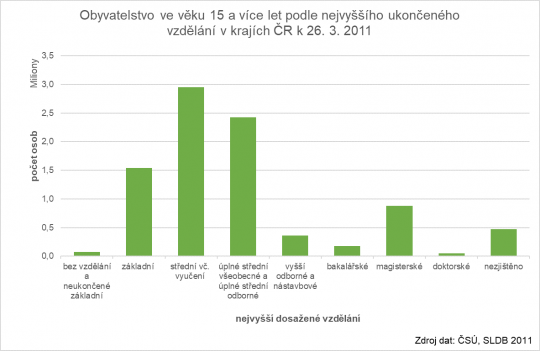
Sloupcový graf použijeme v případě, že chceme zobrazit rozdělení četností kategoriální (slovní) proměnné nebo nespojité kvantitativní proměnné. Na osu X zapisujeme kategorie výsledků (např. nejvyšší dosažené vzdělání, pohlaví, počet dětí v rodině, barvu auta respondenta atp.). Četnost zastoupení jednotlivých výsledků znázorňuje výška sloupců, která může být vyjádřena jak absolutně, tak relativně. Čím je sloupec vyšší (zobrazeno na ose Y), tím je daná kategorie, výsledek, zastoupena v souboru více. U sloupcového grafu se jednotlivé sloupce nedotýkají, viz obrázek 10.
Obr. 10. Sloupcový graf
Doporučuji také podívat se na kapitolu Jak (ne)zkazit sloupcový graf v této online knize [2].
HISTOGRAM ROZDĚLENÍ ČETNOSTÍ
Histogram je speciální variantou sloupcového grafu pro intervalové rozdělení četností. Stejně jako u sloupcového grafu se na ose X vyznačují meze intervalů sledované proměnné a na osu Y se zobrazují četnosti hodnot v daných intervalech. Příkladem dat rozdělených do kategorií mohou být počty odpracovaných hodin nebo mzdy zaměstnanců, oboje rozdělené do intervalů. I zde platí, čím je sloupec vyšší (zobrazeno na ose Y), tím je daný interval hodnot zastoupen v souboru více. U histogramu je důležité si zapamatovat, že jednotlivé sloupce se navzájem dotýkají, protože jde o zobrazení intervalového rozdělení četností.
+
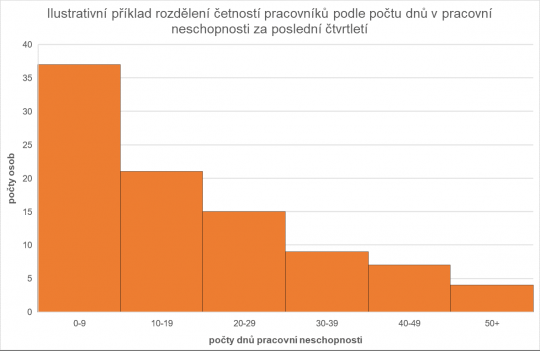
Obr. 11. Histogram rozdělení četností
POLYGON ROZDĚLENÍ ČETNOSTÍ
Polygon četností je spojnicový graf pro kvantitativní proměnnou. Konstruuje se jednoduše tak, že spojíme úsečkami body o souřadnicích xi (zobrazeny na ose X) a ni (zobrazeny na ose Y). „Na ose X vyznačují středy intervalů pro hodnoty sledované proměnné (případně jednotlivé hodnoty kvantitativní proměnné, kterou lze obecně považovat za spojitou) a na osu Y se nanášejí odpovídající četnosti (absolutní nebo relativní). U intervalového rozdělení četností vznikne vlastně spojením středů horních hran jednotlivých sloupců u histogramu.“ [3]
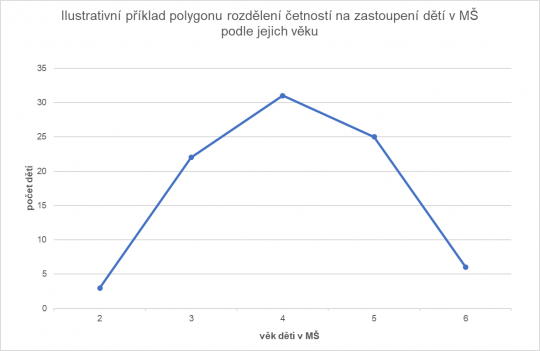
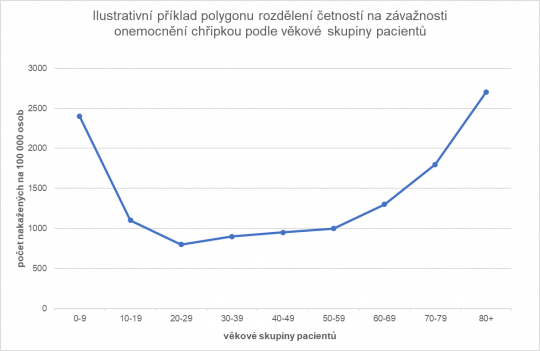
Jaký má rozdělení četností celkový tvar, je ve statistice velmi důležité. Dle toho, kolik má rozdělení vrcholů, můžeme rozlišit jednovrcholová rozdělení četností a vícevrcholová rozdělení četností. Nejčastěji se vyskytují jednovrcholová, resp. unimodální rozdělení četností, u kterých se modus nachází mezi minimální a maximální obměnou proměnné, viz obrázek 12.
Obr. 12. Polygon rozdělení četností
Druhým typem unimodálního rozdělení, kde se nejvyšší četnost nachází u minimální nebo naopak maximální obměny proměnné, je tzv. J-křivka, resp. rozdělení „J“.
+
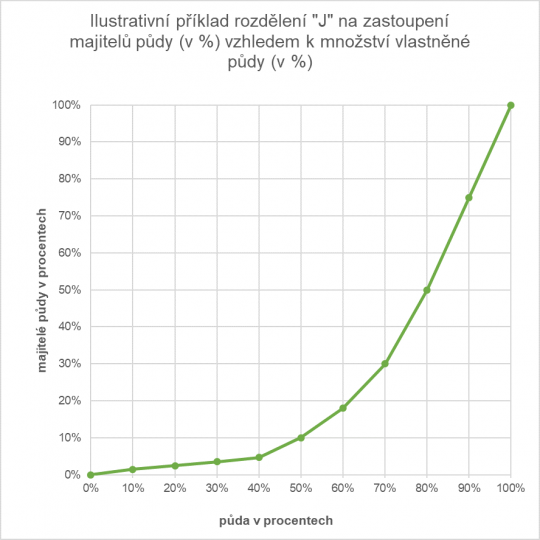
Obr. 13. Schéma rozdělení četností „J“
Vícevrcholové rozdělení četností nebo také multimodální rozdělení četností má více než jeden vrchol, tedy více modů. Pokud má rozdělení dva mody, hovoříme o bimodálním rozdělení četností.
Speciálním typem bimodálního rozdělení je tzv. U-křivka, resp. rozdělení „U“. „U rozdělení ‚U‘ je pro charakterizování polohy rozdělení četností důležitá obměna s nejmenší četností, kterou nazýváme antimodus.“ [1]
+
Obr. 14. Schéma rozdělení četností „U“
Poznámka
„Větší počet vrcholů rozdělení četností než jeden má většinou původ v stejnorodosti zkoumaného statistického souboru, z něhož bývá v takovém případě možné a většinou i nutné vytvořit vhodným roztříděním tolik statistických souborů, kolik mělo původní rozdělení četností vrcholů. Takto lze převést většinu více vrcholových rozdělení četností na obvyklá jednovrcholová rozdělení četností.“ [1]
I u tohoto typu grafu mohu doporučit kapitolu Nespojujme nespojitelné v online knize [2], abychom se vyhnuli špatnému používání polygonu četností.
VÝSEČOVÝ GRAF
Pokud zkoumáme nominální proměnnou, pak pro její zobrazení může být vhodný výsečový graf. Relativní zastoupení jednotlivých obměn (kategorií) proměnné znázorníme pomocí výsečí kruhu. Čím větší je výseč grafu, tím je daná kategorie sledované proměnné zastoupena více. „Ve výsečovém grafu bývá zvykem udávat, u kolika jednotek (případně z kolika procent) je daná kategorie zastoupena.“ [3] Místo pojmu výsečový graf se také můžeme setkat s označením koláčový graf, neboť tyto grafy mnohdy připomínají koláče. Velmi pěkný popis toho, jak by měl vypadat výsečový graf a kdy je vhodné použít raději jiný typ grafu, najdete v kapitole Trable s koláči v této online publikaci [2].
+
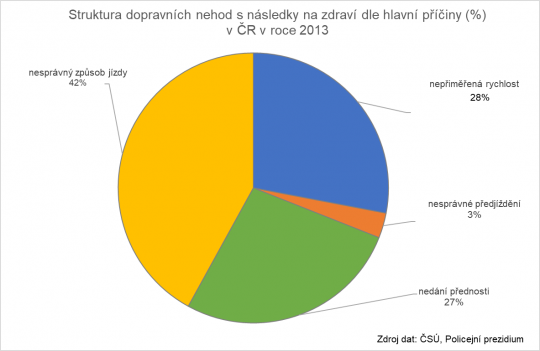
Obr. 15. Výsečový graf
KRABIČKOVÝ GRAF
Krabičkový graf můžeme použít ke znázornění některých souhrnných charakteristik kvantitativní proměnné nebo také proměnné ordinální, jestliže jsou její výsledky vyjádřeny číselně. Tento graf se využívá ke znázornění extrémních hodnot souboru a také hodnot kvartilů. „Obvykle se zobrazují kvartily, tj. 25% kvantil (dolní hrana krabičky), 50% kvantil (bod uvnitř krabičky) a 75% kvantil (horní hrana krabičky), a krajní hodnoty v souboru, tj. minimální (začátek spodního ‚vousu‘) a maximální (konec vrchního ‚vousu‘). V krabičkovém grafu se také znázorňují extrémní a odlehlé hodnoty jako samostatné body (stanovují se na základě kvartilového rozpětí).“ [3] Krabičkový graf je možné znázornit jak vertikálně, tak horizontálně. Někdy bývá označován anglickým výrazem „box-plot“.
+
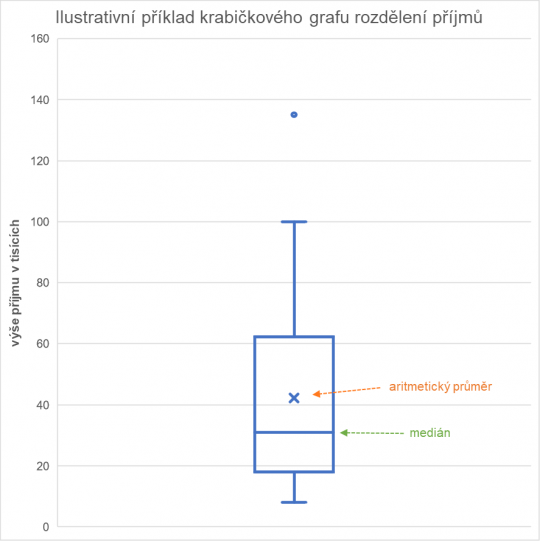
Obr. 16. Krabičkový graf
Poznámka
„Často je vhodná a účelná souběžná vizuální analýza více krabičkových grafů najednou konstruovaných buď pro různé statistické znaky jednoho statistického souboru, anebo pro jeden statistický znak, sledovaný v různých statistických souborech.“ [1]