2.2
Součástky lineární a nelineární
Rozdělení součástek na lineární a nelineární souvisí s tvarem (průběhem) jejich charakteristiky. Charakteristika součástky je grafické zobrazení závislosti jedné obvodové veličiny daného prvku na veličině druhé. V další části textu se zaměříme na součástky odporového charakteru. U odporových prvků je charakteristickou vlastností odpor a základními obvodovými veličinami napětí a proud. Název základní charakteristiky odporových prvků je odvozen od jednotek jejich obvodových veličin (napětí → VOLT, proud → AMPÉR). Jejich charakteristiku označujeme jako voltampérovou. Často ji při popisu a v odborné literatuře najdeme pouze pod zkratkou VACH.
2.2.1
Voltampérová charakteristika (VACH)
+
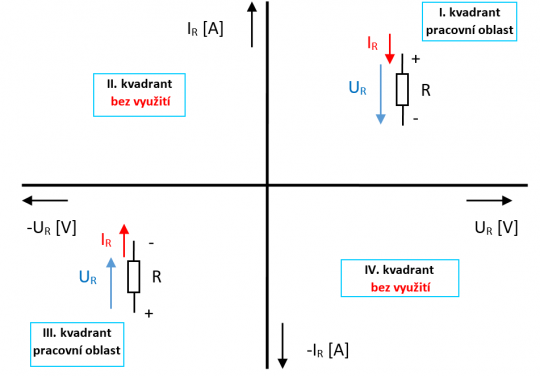
Obr. 9. VACH odporových prvků
Charakteristika má následující vlastnosti:
- Rovina je rozdělena do čtyř kvadrantů.
- Jednotlivé kvadranty označujeme: I., II., III. a IV. kvadrant.
- Střed osy x a y označujeme jako počátek souřadného systému.
- Na osu x vyznačujeme napětí daného prvku (od počátku vpravo kladné +U, vlevo záporné -U).
- Na osu y vyznačujeme proud daného prvku (od počátku nahoru kladný +I, dolů záporný -I).
- Charakteristika je tvořena nekonečně velkým množstvím bodů.
- Každý elementární bod charakteristiky odpovídá hodnotě napětí (osa x) a hodnotě proudu (osa y) daného odporového prvku.
2.2.2
Voltampérová charakteristika lineárních odporových prvků
Typickým průběhem VACH lineárních prvků je přímka.
+
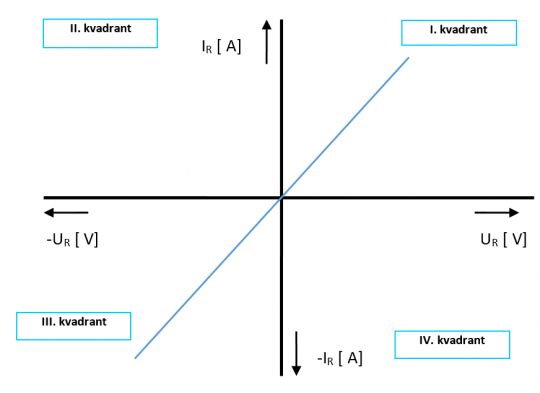
Obr. 10. VACH lineárních prvků
Z výše uvedené charakteristiky může definovat tyto vlastnosti:
- Charakteristika prochází pouze I. a III. kvadrantem (pasivní odporový prvek).
- Průběh VACH je přímka, která prochází počátkem.
- Ke konstrukci celé charakteristiky potřebujeme pouze jeden bod v rovině I. nebo III. kvadrantu (druhý bodem je počátek souřadného systému).
- Sklon VACH (úhel mezi osou x a charakteristikou) je nepřímo úměrný velikosti odporu.
V elektrotechnice patří mezi základní dovednosti voltampérovou charakteristiku narýsovat nebo z této charakteristiky odečíst důležité parametry. Na následujících dvou příkladech si tyto dovednosti ukážeme.
Příklad
Nakreslete VACH dvou lineárních rezistorů R1 = 1 kΩ a R2 = 2 kΩ. Hodnoty napětí na ose x zvolte v rozsahu 0 až ±5 V.
Zobrazit řešení
Řešení
Pro konstrukci charakteristiky potřebujeme pouze jeden další bod. Jedním bodem je totiž vždy střed charakteristiky (nulový proud a nulové napětí). Druhým bodem je libovolná odpovídající si dvojice napětí a proudu v rovině (I. nebo III. kvadrant).
Pro rezistor R1 zvolíme napětí UR1 = 1 V, pro rezistor R2 pak UR2 = 2 V (pro tuto volbu napětí bude výpočet proudu výrazně jednoduchý).
+
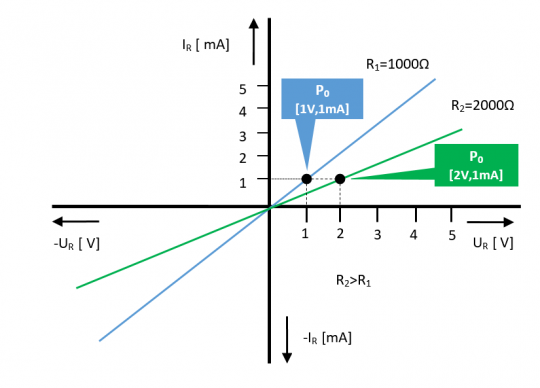
Obr. 11. VACH rezistorů R1, R2 (příklad)
Příklad
Na VACH neznámého rezistoru zvolte libovolné tři body (A, B, C) a v každém z nich odečtěte hodnotu napětí UR, hodnotu proudu IR a odpovídající velikost hodnoty odporu R. Výsledné hodnoty rezistoru porovnejte a slovně zhodnoťte. Polohu bodů A, B, C volte v celém rozsahu definované charakteristiky → I. a III. kvadrant.
Zobrazit řešení
Řešení
V bodě A charakteristiky odečteme napětí a proud na rezistoru:
V bodě B charakteristiky odečteme napětí a proud na rezistoru:
V bodě C charakteristiky odečteme napětí a proud na rezistoru:
Po porovnání výsledků můžeme konstatovat, že výsledek všech tří výpočtů je přibližně stejný. Drobné odchylky jsou dány nepřesností odečtu napětí a proudu na osách x a y. Stejná hodnota odporu v každém bodě VACH rezistoru odpovídá teoretickým vlastnostem rezistoru.
+
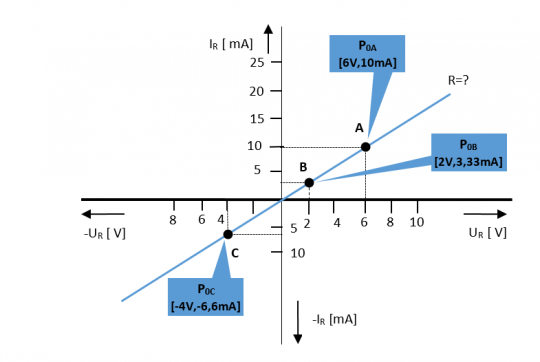
Obr. 12. Příklad VACH, výpočty v bodech A, B, C
2.2.3
Voltampérová charakteristika nelineárních prvků
Průběh VACH nelineárních prvků je nelineární závislost.
+
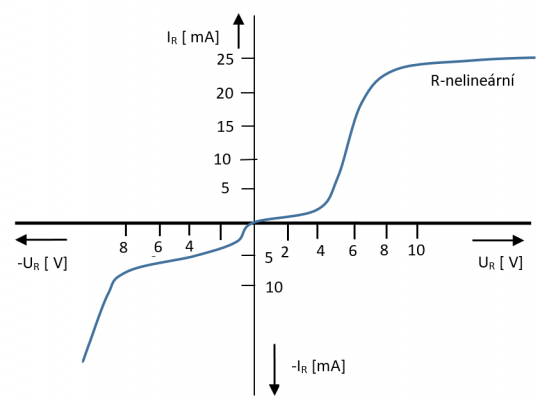
Obr. 13. VACH nelineárních prvků
Pro popis a konstrukci VACH platí stejné vlastnosti, jako má VACH lineárních prvků, pouze průběh vlastní charakteristiky je nelineární.
2.2.4
Parametrické VACH prvků
U některých nelineárních prvků není v rovině VACH (kvadrant I, II, III, IV) pouze jedna charakteristika. Typickým příkladem je charakteristika bipolárního tranzistoru. V prvním kvadrantu, který popisuje výstupní vlastnosti tranzistoru, není pouze jedna charakteristika, ale nekonečné množství charakteristik (jejich parametrem je vstupní proud tranzistoru (IB – proud báze). Parametrem charakteristik může být teplota prvku nebo intenzita vnějšího osvětlení dopadajícího na prvek.
+
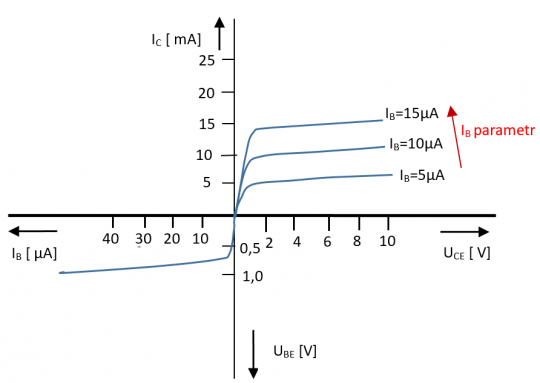
Obr. 14. VACH parametrických prvků
2.2.5
Odečet parametrů z VACH
Každá charakteristika v elektrotechnice představuje soubor nekonečného množství bodů. Jeden elementární bod VACH jednoznačně definuje obvodové veličiny, které na daný prvek (součástku) působí. Nejčastěji jsou těmito veličinami napětí a proud (může být napětí a napětí nebo proud a proud). Hodnota jednoho napětí na prvku a jednoho proudu procházejícího prvkem definují pracovní režim. Často hovoříme o pracovním bodu (jednom bodu charakteristiky). V daném pracovním bodě můžeme popsat vlastnosti prvku několika různě definovanými parametry.
2.2.5.1
Statický parametr
Je definován jako poměr klidových hodnot obvodových veličin v daném pracovním bodě nebo v libovolném bodě charakteristiky.
+
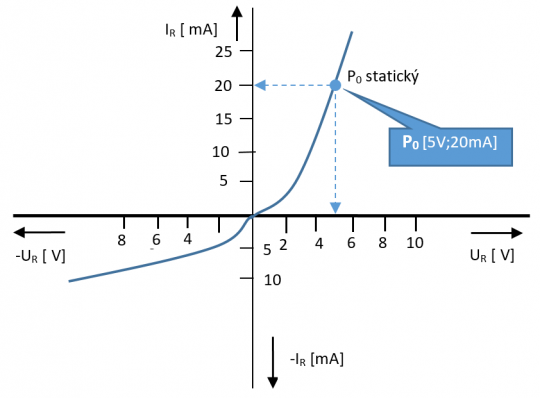
Obr. 15. Definice statického parametru charakteristiky
Statický parametr odečtený z charakteristiky představuje odpor s hodnotou (napětí/proud). Tento lineární odpor má s nelineárním prvkem stejné parametry ve dvou bodech (počátek souřadného systému VACH a právě tento bod).
2.2.5.2
Dynamický (diferenciální) parametr
Tato metoda odečtení parametru z VACH je metodou graficko-početní. V pracovním bodě P0 na VACH se nakreslí tečna. Na tečně (přímce) se zvolí dva body a provede se promítnutí na osu x a y. Z odečtených hodnot napětí na ose x a proudu na ose y se vypočítá změna napětí ΔU a změna proudu ΔI. Dosazením do vzorce (dle Ohmova zákonu) se vypočítá hodnota dynamického odporu.
+
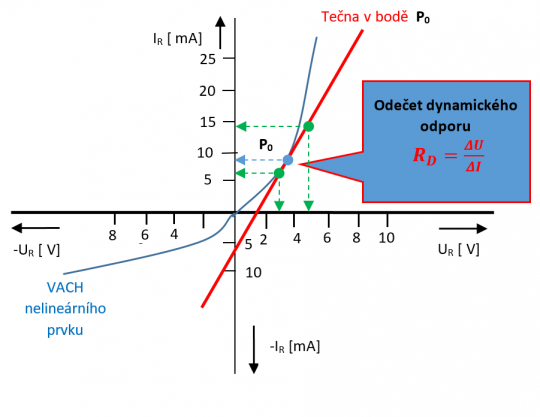
Obr. 16. Definice dynamického (diferenciálního) parametru