1.1
Popis sekvenčního logického obvodu
Činnost sekvenčního logického obvodu můžeme popsat několika různými způsoby [3].
1. Algebraický způsob
Popisuje pomocí množiny Booleovských rovnic pro přechodové funkce G a výstupní funkce F, které jsme si uvedli na začátku této kapitoly. Podle závislosti výstupní funkce obvodu rozlišíme snadno obvod typu Mealy a typu Moore [4].
,
– pro typ Mealy,
– pro typ Moore.
2. Tabulka přechodů a výstupů
Představuje tabulkové vyjádření hodnot přechodů vnitřních stavů a výstupů obvodu na základě vstupů a vnitřních stavů. Obě tabulky s výhodou spojujeme do jedné, rozdělné na dvě části. Příklad obecného uspořádání tabulek pro obvod typu Mealy a Moore ukazuje obrázek 2.
+
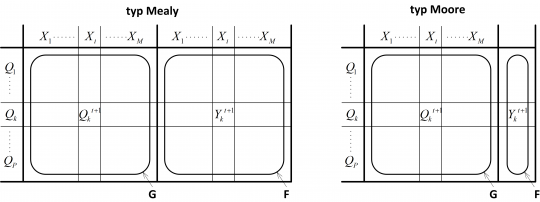
Obr. 2. Obecné uspořádání tabulek přechodů a výstupů pro obvody Mealy a Moore.
Zopakujme si indexy z algebraické definice sekvenčního obvodu: m vstupních stavů obvodu, p vnitřních stavů obvodu, n výstupních stavů obvodu [4].
Pro oba typy (Mealy i Moore) mají tabulky vždy p řádků – p vnitřních stavů obvodu.
Tabulka pro typ Mealy
- Počet sloupců tabulky = 2 × m, tj. 1 × m sloupců pro přechodové funkce + 1 × m sloupců pro výstupní funkce.
- Počet výstupních stavů obvodu = m × p.
Tabulka pro typ Moore
- Počet sloupců tabulky = 1 × m + 1, tj. 1 × m sloupců pro přechodové funkce + 1 sloupec pro výstupní funkce.
- Počet výstupních stavů obvodu = 1 × p.
Pokud pro některou kombinaci vnitřního a vstupního stavu obvodu není určena přechodová či výstupní funkce obvodu a jedná se tedy o neurčitý stav obvodu, značíme jej v tabulce obvykle symbolem „-“ a hovoříme o tzv. neúplně určeném obvodu. Pokud jsou naopak všechny kombinace jednoznačně určeny, jedná se o úplně určený obvod.
Poznámka
Výše uvedené tabulky ještě obvykle pro úplnost doplňujeme o tzv. počáteční stav obvodu q0 v čase t = 0 [4].
3. Orientovaný graf přechodů
Někdy též označovaný jako přechodový diagram či stavový diagram, představuje grafický způsob popisu činnosti sekvenčního logického obvodu [5].
Graf obsahuje p uzlů, které představují vnitřní stavy obvodu (p vnitřních stavů obvodu). A dále je v grafu použito p + n orientovaných hran mezi těmito uzly (p + n = p vnitřních stavů + n výstupů obvodu).
Graf pro typ Mealy
- Výstupy obvodu Y jsou uvedeny na hranách grafu. Každá orientovaná hrana je označena dvojicí xi, yi vyjadřující vstupní stav obvodu inicializující přechod z vnitřního stavu qi do stavu qj s daným výstupem obvodu yi.
Graf pro typ Moore
- Výstupy obvodu Y jsou určeny pouze aktuálním vnitřním stavem Q. Z tohoto důvodu jsou výstupní stavy v případě Mooreova typu uvedeny v uzlech grafu společně s vnitřními stavy obvodu. Každá orientovaná hrana grafu je pak označena pouze vstupním stavem xi, který způsobí přechod obvodu z vnitřního stavu qi do stavu qj, a po jeho dosažení je na výstupu obvodu stav yi.
Ukázku části grafu přechodů pro typ Mealy a pro typ Moore ilustruje obrázek 3.
+

Obr. 3. Ukázka části grafu přechodů pro obvody Mealy a Moore.
4. Slovní popis (časový diagram)
Používá se pro slovní definici a popis funkce sekvenčního obvodu například při zadání úlohy pro jeho syntézu. Slovní popis obvodu bývá často doprovázen jeho časovým diagramem pro lepší vymezení funkce obvodu [4].
5. Popis chování či struktury sekvenčního obvodu v jazycích VHDL či Verilog
Blíže je tato možnost rozvedena v textu „Úvod do jazyka VHDL III“.
6. Popis funkce sekvenčního obvodu vývojovým diagramem
Jedná se často o standardizované grafické značky, příkladem je jazyk UML (Unified Modeling Language) [1].