3.1
Statický hazard a jeho odstranění
V předchozí kapitole jsme si uvedli definici statického hazardu. Z hlediska hodnoty výstupní funkce obvodu rozlišujeme dva základní typy – statický hazard v logické jedničce a statický hazard v logické nule. Pokud bychom připojili dostatečně rychlý osciloskop k výstupu obvodu a navodili hazardní stav, rozlišili bychom oba typy statického hazardu dle výstupu na osciloskopu, jak ukazuje obrázek 15.
+
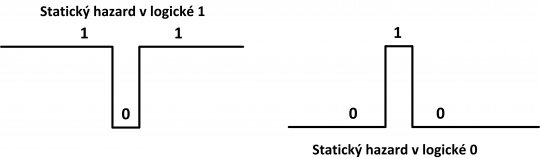
Obr. 15. Statický hazard v logické 1 a logické 0 zobrazený na osciloskopu.
Souhrn
V případě statického hazardu v logické 1 se na krátký časový okamžik na výstupu obvodu objeví hodnota logická 0, ačkoliv by výstup obvodu měl setrvávat stále na hodnotě logická 1. Naopak statický hazard v logické 0 je charakterizován tím, že se výstup obvodu na krátký časový okamžik při přechodu změní na hodnotu logická 1, ačkoliv by měl setrvávat na hodnotě logická 0.
Definice
Statický hazard v logické 1 vzniká pouze v obvodu složeném ze součinových logických hradel, tedy AND, NAND, zatímco statický hazard v logické 0 vznikne pouze v obvodu obsahujícím součtová logická hradla, tzn. OR a NOR.
Uveďme si příklad obvodu obsahujícího logický hazard, možnosti jeho analýzy a eliminace.
Příklad
Realizujte formu MNDF funkce f čtyř proměnných pomocí hradel NAND. Proveďte vyšetření obvodu na vznik statického hazardu a případný hazard eliminujte.
f = 1, 3, 5, 7, 8, 9, 12, 13.
Zobrazit řešení
Skrýt řešení
Řešení
Použijeme Karnaughovu mapu pro čtyři proměnné, do které vyplníme zadané jednotkové body funkce f, nalezneme co největší smyčky, abychom pokryli všechny jednotkové body a získali tak formu MNDF funkce. Výsledné řešení je uvedeno na obrázku 16.
+
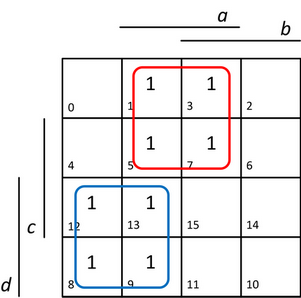
Obr. 16. Karnaughova mapa pro nalezení formy MNDF zadané funkce.
Formu MNDF upravíme pro realizaci pomocí hradel NAND:
.
Pro realizaci negací vstupních proměnných d a b budeme potřebovat dvě hradla NAND, další tři hradla NAND pak na realizaci vlastní funkce f, jak ukazuje obrázek 17.
+
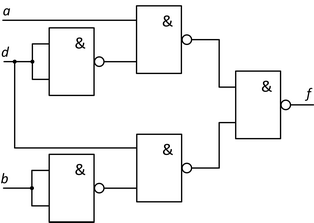
Obr. 17. Realizace formy MNDF zadané funkce pomocí hradel NAND.
Nyní obvod vyšetříme na přítomnost logických hazardů. Protože je relativně jednoduchý a existují v něm jen dvě větve hradel a protože je realizován ze součinových hradel NAND, zaměříme se pouze na statický hazard v logické jedničce. K jeho detekci vyjdeme ze dvou indicií.
- Proměnná d se ze vstupu obvodu na jeho výstup šíří dvěma různými cestami a tyto cesty obsahují různý počet hradel. Z toho vyplývá, že doba zpoždění při průchodu proměnné d těmito cestami bude různá. (Obvod jsme zakreslili schválně tímto způsobem, abychom snadno určili stupeň obvodu – počet hradel mezi vstupem a výstupem jednotlivých větví.)
- V Karnaughově mapě si můžeme povšimnout přechodu mezi stavy (políčky) číslo 5 a 13. Pro obě políčka nabývá hodnota výstupní funkce logické jedničky, políčka spolu navzájem sousedí, ale náleží každé do jiné smyčky. Navíc dle bodu výše nabývá hodnota vstupní proměnné d pro políčko číslo 5 logické 0, pro políčko 13 naopak logické 1.
Díky tomuto předpokladu se budeme zajímat o přechod mezi stavy (políčky) číslo 5 a 13. Jednotlivé vstupní proměnné nabývají hodnot dle tabulky 10.
Tabulka 10. Hodnoty vstupních proměnných zadané funkce při vzniku statického hazardu v logické 1.
Stav (políčko) | d | c | b | a |
5 | 0 | 1 | 0 | 1 |
13 | 1 | 1 | 0 | 1 |
Z tabulky vyplývá, že proměnné a, b, c mají konstantní hodnoty při přechodu mezi těmito dvěma stavy, proměnná d se však mění.
Nyní sestavíme tzv. časový diagram obvodu, abychom vyšetřili, zda k hazardu skutečně dochází.
Časový diagram obvodu představuje jednoduchou časovou analýzu průběhu signálů na výstupech jednotlivých hradel a na výstupu obvodu. V podstatě si jej můžeme představit, jako kdybychom připojili sondu osciloskopu do jednotlivých bodů obvodu (na výstupy jednotlivých hradel) a zkoumali časový průběh v těchto bodech při přechodu mezi vyšetřovanými stavy. Pro sestavení časového diagramu přijmeme zjednodušení situace – všechna logická hradla mají stejné zpoždění o velikosti ΔT. Postup sestavení časového diagramu vystihuje následující animace 1.
Animace 1. Animace sestavení časového diagramu pro vyšetření obvodu na vznik logického hazardu.
Výsledný časový diagram se znázorněním okamžiku vzniku statického hazardu v logické 1 v daném obvodu je uveden na obrázku 18.
+
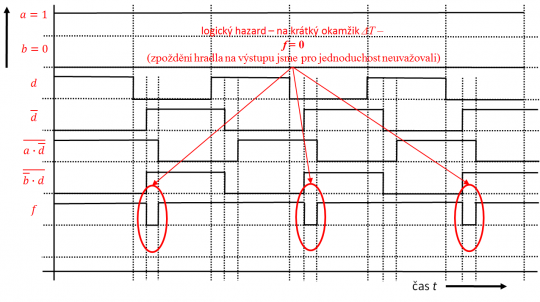
Obr. 18. Vznik statického hazardu v logické 1 v daném obvodu.
Sestaveným časovým diagramem jsme potvrdili, že v obvodu vzniká pro přechod funkce mezi stavy 5 a 13 při vstupní kombinaci proměnných v tabulce 10 statický hazard v logické 1.
Dalším krokem je tedy daný statický hazard odstranit. Použijeme k tomu strukturální úpravu obvodu. V Karnaughově mapě nalezené formy MNDF funkce na obrázku 16 si můžeme povšimnout, že kritická políčka 5 a 13 můžeme obě pokrýt pomocí dodatečné smyčky tvořené políčky 1, 5, 13 a 9, které odpovídá prostý implikant
. Tento implikant navíc neobsahuje proměnnou d, jejíž změna daný hazard způsobila. V Karnaughově mapě vyznačíme tedy tuto dodatečnou smyčku zeleně, jak ukazuje obrázek 19 (vlevo). V témže obrázku vpravo je pak uvedena upravená realizace obvodu pomocí hradel NAND, která vychází z upravené disjunktní formy funkce (ta již však není minimální!):
.
+
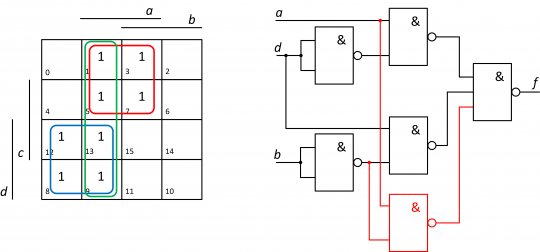
Obr. 19. Vyznačení dodatečné smyčky v Karnaughově mapě pro odstranění statického hazardu v obvodu (vlevo) a upravený obvod realizovaný pomocí hradel NAND s eliminací statického hazardu v logické 1 (vpravo).
Ve schématu je dodatečné hradlo NAND doplněné pro realizaci nové smyčky (a implikantu) zakresleno červeně, výstupní hradlo NAND je nyní potřeba zvolit se třemi vstupy.
Abychom ověřili, zda tato úprava opravdu pomohla odstranit nalezený statický hazard, sestavíme opět časový diagram pro takto upravený obvod na obrázku 19. Jeho vytvoření je uvedeno v animaci 2. Původní průběhy signálů, které jsou stejné i v nově upraveném obvodu, jsou z původní animace 1 pouze převzaty a animace 2 tedy uvádí jen průběhy nových signálů pro upravený logický obvod.
Animace 2. Animace sestavení časového diagramu pro upravený obvod s eliminací logického hazardu.
Výsledný časový diagram sestavený pro upravený obvod s doplněním dodatečného hradla NAND pro eliminaci statického hazardu v logické 1 je uveden na obrázku 20.
+
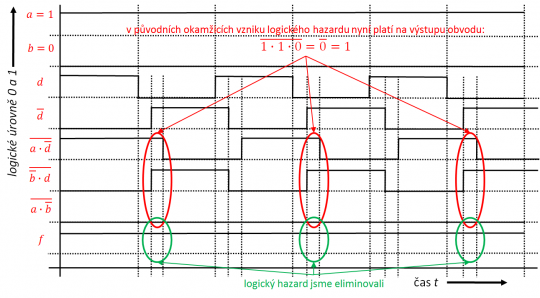
Obr. 20. Časový diagram obvodu s eliminací statického hazardu v logické 1.
Ze sestaveného časového diagramu vyplývá, že se nám podařilo statický hazard v logické 1 úspěšně eliminovat. Prostý implikant
totiž neobsahuje vůbec proměnnou d a jeho hodnota se tedy při přechodu mezi stavy (políčky) 5 a 13 nemění a zůstává konstantně logická 0. Do výstupního hradla NAND nyní vstupují tři signály – původní dva obsahující proměnnou d a tedy se měnící mezi hodnotami logická 0 a 1, jak ukazuje časový diagram, a dále signál s konstantní hodnotou logická 0. Protože se jedná o součinové hradlo NAND, je výstupem vždy logická 1 (logická 0 krát cokoliv a z toho negace = logická 1). Ke vzniku krátkého překmitu (hazardu) do hodnoty logická 0 tedy již nikdy nedojde.
Nevýhodou této úpravy obvodu a eliminace původního hazardu však je, že se již nejedná o minimální formu MNDF a její realizaci. Obvod obsahuje jedno hradlo NAND navíc.