Kapitola1
Definice kombinačního logického obvodu
V úvodním textu „Úvod do logických funkcí a logických obvodů“ jsme si definovali pojem obecný logický obvod.
Souhrn
Logický obvod je obecně elektronický obvod složený z logických hradel, který umožňuje zpracovávat logické signály [1]. Dále jsme se omezili na, v praxi nejpoužívanější, tzv. dvouhodnotovou logiku, tedy logické obvody, které pracují se dvěma stavy, logickou 1 a logickou 0.
Na základě činnosti a vnitřní struktury lze logické obvody rozdělit na dvě základní skupiny, tzv. kombinační obvody a sekvenční obvody [1].
K definici obecného kombinačního logického obvodu využijeme následující obrázek 1.
+
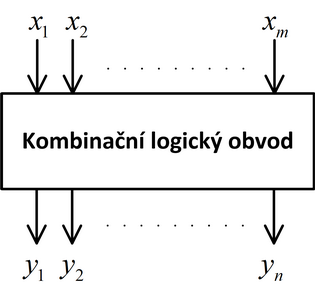
Obr. 1. Obecné schéma kombinačního logického obvodu.
Definice
Každý kombinační logický obvod jednoznačně definuje:
- množina vstupních logických proměnných (logických vstupů obvodu) X = x0, x1, x2, x3, …., xn-1,
- množina výstupních logických proměnných (logických výstupů obvodu) Y = y0, y1, y2, …, ym-1.
Kde obecně n ≠ m, obvod tedy může mít obecně různý počet vstupů a výstupů.
Pro takový obvod můžeme definovat množinu tzv. výstupních funkcí obvodu F = f0, f1, f2, …, fm-1.
Hodnoty výstupních proměnných (výstupů kombinačního logického obvodu) jsou pak jednoznačně určeny: Y = F(X), tzn.: y1 = f1(x0, x1, x2, x3, …, xn-1), y2 = f2(x0, x1, x2, x3, …, xn-1), …, ym-1 = fm-1(x0, x1, x2, x3, …, xn-1).
Pro kombinační logický obvod tedy platí, že v každém okamžiku jsou hodnoty na jeho výstupech Y jednoznačně určeny současnou hodnotou (kombinací) vstupů obvodu X pomocí jeho výstupních funkcí F [1].
Poznámka
V tom se kombinační logický obvod liší od sekvenčního logického obvodu, který má navíc tzv. vnitřní stavy a jeho výstupní hodnota je tedy obecně kromě vstupní hodnoty závislá i na vnitřním stavu (stavech) obvodu [1].
Sekvenční logický obvod má kromě své kombinační části i tzv. paměťovou část sloužící k uchování informace o jeho vnitřním stavu [1].
Navíc se pro řízení tzv. přechodů mezi vnitřními stavy sekvenčního logického obvodu může uplatnit i hodinový (periodický) signál, a rozlišujeme tedy sekvenční logické obvody synchronní (časované hodinovým signálem) a asynchronní (bez časového signálu). Více o sekvenčních logických obvodech pojednává navazující text „Sekvenční logické obvody, klopné obvody a stavové automaty“.
Typickými zástupci sekvenčních logických obvodů jsou čítače, registry, obvody pro práci s hodinovým taktem, konečné stavové automaty apod.
Pro výstupní funkce kombinačního logického obvodu F můžeme tedy sestavit množinu Booleových rovnic a popsat jimi funkci obvodu. Kromě nich lze obecně funkci kombinačního logického obvodu popsat pomocí:
- pravdivostní tabulky – ta udává převod vstupních kombinací obvodu na jeho výstupy,
- schématem obvodu – pomocí schématických značek logických hradel a základních bloků lze zakreslit vnitřní uspořádání obvodu,
- mapami, tělesy a dalšími grafickými prostředky,
- slovním popisem funkce obvodu.
Kombinační logické obvody nalezneme v nejrůznějších aplikacích a jejich využití je mnohostranné [2].
Příklad
V praxi mezi nejčastěji používané kombinační obvody patří zejména:
- multiplexory, demultiplexory,
- kodéry a dekodéry,
- převodníky kódů (z BCD na různé binární kódy), převodníky kódů pro segmentové displeje,
- binární sčítačky (úplné a neúplné), násobičky, děličky,
- komparátory, paritní kodéry a dekodéry, realizace logických operací apod.
Poznámka
Všechny doposud uvedené logické obvody a nakreslená schémata logických obvodů v textech „Úvod do logických funkcí a logických obvodů“, „Minimalizace logických funkcí pomocí zákonů Booleovy algebry a Karnaughových map“ a „Minimalizace logických funkcí pomocí těles a algoritmu Quine-McCluskey“ byly kombinační logické obvody.