3.2
Metody řešení elektronických obvodů
3.2.1
Ideální a skutečný zdroj elektrické energie
Ideální nezávislý zdroj napětí
Ideální nezávislý zdroj napětí je aktivní jednobran (dvojpól), jehož zatěžovací charakteristikou je přímka rovnoběžná s osou proudu. Velikost napětí tohoto zdroje není nezávislá na velikosti zatěžovacího proudu ani na čase, případně dalších veličinách. Je schopen dodávat nekonečně velký výkon (proud), přičemž velikost napětí se nemění, zatímco skutečné zdroje jsou schopné dodávat pouze omezený výkon (proud). Na rozdíl od reálného zdroje vykazuje nulový vnitřní odpor.
+

Obr. 3. Zatěžovací charakteristika ideálního zdroje napětí
Reálné stejnosměrné zdroje
Každý obvod obsahující zdroj stejnosměrného napětí nebo proudu a odporový obvod můžeme považovat za reálný stejnosměrný zdroj napětí nebo proudu. Reálné stejnosměrné zdroje elektrické energie je možné modelovat kombinací ideálních zdrojů a rezistorů. To má vliv na jejich zatěžovací charakteristiky.
Charakteristická rovnice reálného stejnosměrného zdroje napětí: U=f(I)
Rovnice vyjadřuje, že velikost výstupního napětí zdroje není konstantní, ale je závislá na velikosti zatěžovacího proudu. Při zatížení proudem IS je na svorkách zdroje napětí US. Velikost výkonu dodávaného ze zdroje do zátěže je P=US*IS. Charakteristickými body na ose napětí a na ose proudu jsou:
- napětí naprázdno UP
- proud nakrátko IK
Napětí naprázdno je napětí naměřené na svorkách zdroje, když není odebírán žádný proud, proud nakrátko je proud dodávaný zdrojem při zkratovaných svorkách.
Napětí naprázdno je největší napětí naměřené na svorkách zdroje. Při zatížení se projevuje vnitřní odpor zdroje, na kterém vzniká úbytek napětí.
+

Obr. 4. Zatěžovací charakteristika reálného zdroje napětí
Zdroj s lineárním vnitřním odporem
Velmi častý je případ, kdy zatěžovací charakteristiky jsou lineární. V tom případě budou v náhradním zapojení nelineární rezistory nebo vodivosti nahrazeny lineárními. Samozřejmě i pro tento případ platí výše uvedené vztahy, hodnoty vnitřního odporu a vnitřní vodivosti jsou konstantní, stačí je vypočítat pouze pro jednu hodnotu zatěžovacího napětí US a zatěžovacího proudu IS.
+

Obr. 5. Zatěžovací charakteristika lineárního reálného zdroje napětí
3.2.2
Théveninova věta
Jakýkoliv (jakkoliv složitý) aktivní lineární jednobran můžeme nahradit jeho ekvivalentním obvodem, který obsahuje ekvivalentní napěťový zdroj UT sériově spojený s ekvivalentním odporem RT.
Podle Théveninovy věty vlastně nahradíme obvod ideálním zdrojem napětí a jeho vnitřním odporem.
+

Obr. 6. Théveninova věta
3.2.3
Metoda smyčkových proudů
Metoda je založena na použití druhého Kirchhoffova zákona, takže je vyloučeno sestavit rovnice, které by byly na sobě závislé. Do každé smyčky zavádíme smyčkový proud.
- smyčkové proudy označíme v každé smyčce libovolně. Tyto smyčkové proudy jsou pro nás neznámé veličiny a musíme sestavit tolik rovnic, kolik je v daném zapojení smyček
- pro každou smyčku sestavíme obvodovou rovnici podle II. K. Z
- každým rezistorem, který je společný dvěma smyčkám, prochází podle zavedeného označení dva proudy
- jsou to proudy obou sousedních smyček, pro něž je rezistor společným prvkem
- doporučuje se volit smysl smyčkových proudů souhlasný, např. ve směru pohybu hodinových ručiček
- výhodné je rovněž postupovat při sestavování rovnic ve smyčkách ve stejném smyslu, pak jsou úbytky napětí v příslušné smyčce kladné, úbytky napětí na sousedních smyčkách záporné
Postup při řešení obvodu metodou smyčkových proudů
- pro každou smyčku sestavíme obvodovou rovnici podle II. K. Z. Tím dostaneme soustavu rovnic
- označíme v každé smyčce smyčkový proud a na každém prvku předpokládaný smysl skutečného proudu
- řešením soustavy rovnic vypočteme smyčkové proudy
- skutečné proudy stanovíme smyčkovými proudy, napětí na jednotlivých prvcích pak vypočteme pomocí Ohmova zákona. Vyjde-li nějaký skutečný proud se záporným znaménkem, je jeho smysl opačný, než jsme předpokládali
+
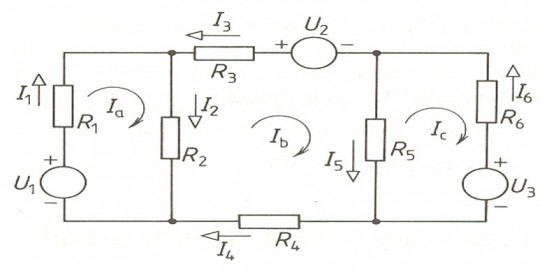
Obr. 7. Metoda smyčkových proudů