2.1
Imitanční parametry
O imitančních parametrech hovoříme za předpokladu, že nezávisle proměnnými jsou buď jen oba proudy, nebo jen obě napětí.
2.1.1
Impedanční charakteristiky
Zvolíme-li za nezávisle proměnné oba proudy, platí vztahy
,
U lineárních dvojbranů jsou tyto vztahy lineární a s výhodou použijeme operátorové vyjádření. Zavedeme-li Laplaceovy obrazy použitých veličin, tj.
,
pak pro nulové počáteční podmínky můžeme psát
,
Parametry
,
,
,
, které se v těchto rovnicích vyskytují, jsou tzv. charakteristiky dvojbranu, jejich rozměr je (
); proto jsme je označili jako impedance. Z toho se také odvozuje, že rovnice se jmenují impedanční. Pro jejich zápis se s výhodou používají matice, tj.:
Proto bylo také použito pro označení charakteristik indexů, které určují jejich polohu v matici. Zavedeme-li následující označení matic, tj.
můžeme zapsat impedanční matici ve tvaru
Matice
se nazývá impedanční matice dvojbranu a můžeme ji pokládat za jeho obecnou charakteristiku.
Při praktických výpočtech je vždy třeba udat zvolené kladné smysly veličin
.
Pro impedanční charakteristiky je zavedena volba podle obrázku 2.
+
Obr. 2. Volba orientací obvodových veličin
Fyzikální význam prvků impedanční matice vyplývá ze stavů dvojbranu naprázdno. Bude-li jeho výstup odpojen od vnějších obvodů, bude
, a proto
a
.
Je tedy:
Podobně bude při odpojení vstupních svorek opět
, a proto
a
.
Odtud vyplývá
Prvky
a
jsou vstupní a výstupní impedance dvojbranu naprázdno a můžeme je u skutečných dvojbranů zjistit přímým měřením impedance mezi příslušnými svorkami.
Prvky
a
jsou definovány poměrem napětí a proudů různých dvojic svorek, a proto je nazýváme přenosovými impedancemi.
Na základě impedančních rovnic můžeme vytvořit náhradní zapojení dvojbranu, které je nezávislé na skutečném vnitřním uspořádání. Je vytvořeno z příslušných prvků impedanční matice a je uvedeno na obr. 3.
+
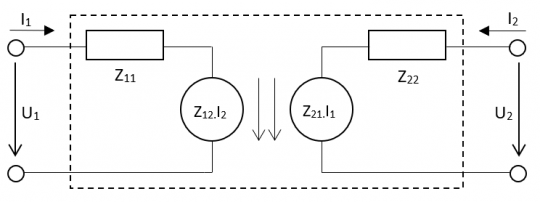
Obr. 3. Náhradní schéma dvojbranu z impedanční matice
Skládá se ze dvou impedancí
a
a ze dvou zdrojů napětí řízených proudy
a
, jimiž je vyjádřen vliv vstupního obvodu na výstupní a naopak.
2.1.2
Admitanční charakteristiky
Zvolíme-li za nezávisle proměnné obě napětí, dostaneme pro nulové počáteční podmínky tzv. admitanční rovnice.
,
Parametry
,
,
,
, které se v těchto rovnicích vyskytují, mají rozměr admitance, tj. [S].
Pro jejich zápis opět použijeme matice:
.
Zavedeme-li následující označení matic, tj.
můžeme zapsat impedanční matici ve tvaru
Fyzikální význam prvků admitanční matice vyplývá ze stavů dvojbranu nakrátko. Při zkratovaných výstupních svorkách bude
, a proto
a
.
Z výše uvedeného vyplývá:
Podobně při zkratování vstupních svorek bude opět
, a proto
a
.
Odtud vyplývá
Prvky
a
jsou vstupní a výstupní admitance dvojbranu nakrátko a můžeme je u skutečných dvojbranů zjistit přímým měřením, prvky
a
jsou definovány poměrem proudů a napětí různých dvojic svorek, a proto je nazýváme impedance přenosové.
Podobně, jako jsme nalezli náhradní zapojení dvojbranu na základě jeho impedančních rovnic, můžeme vytvořit náhradní zapojení dvojbranu rovněž na základě rovnic admitančních, viz obr. 4.
+
Obr. 4. Náhradní schéma dvojbranu z admitanční matice
Pro impedanční i admitanční rovnice používáme stejné volby kladných smyslů napětí a proudů.